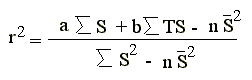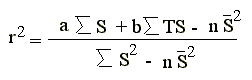Solutions to Assignment #3 and #4

• Problem 12-9
• Problem 12-21
• Problem 12-30
• Problem 12-33
• Problem 12-37
• Problem 13-30

• a) Linear and direct
• b) Curvilinear and inverse
• c) Curvilinear and inverse

• a) Calculation of the regression parameters:

	T	S	T*S	T2
	2.6	95	247	6.76
	3.7	140	518	13.69
	2.4	85	204	5.76
	4.5	180	810	20.25
	2.6	100	260	6.76
	5.0	195	975	25.00
	2.8	115	322	7.84
	3.0	136	408	9.00
	4.0	175	700	16.00
	3.4	150	510	11.56
Total	34.0	1371	4954	122.6

b= (4954 - 10 * 3.4 * 137.1)/(122.6 - 10 * 3.4²) = 41.6809
a= 137.1 - 41.6809 * 3.4 = - 4.6151

The estimated regression line is then S = -4.6151 + 41.6809 * T

• b) The question is about the slope of the estimated line. Sales appear to increase by 41.68 units per point increase in test score

 

 
 
 

• c) S = -4.6151 + 41.6809 * 3.4 = 137.1

 

 
 
 
 

Click for Excel Regression output
To Top

The easiest way to calculate the coefficient of determination is to use the computational formula:

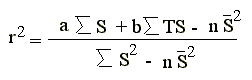
All the quantities needed in this formula with the exception of the "sum of squared S" is already on hand from the solution of 21. Sum of squared-S (first square the S values then sum) is 201,121.

r² = (-4.6151*1371 + 41.6809 * 4954 - 10 * 137.1 * 137.1)/(201,121 - 10 * 137.1* 137.1) = 0.92695

The Sample Correlation Coefficien is the square-root or r = 0.96278
To Top

• n= 25
• b= 1.12
• s_e=8.516
• (SX² - n X ²) = 327.52

---

• a) s_b = s_e[(1/(SX² - n X ²) ]^1/2 = 8.516 * (1/327.52)^1/2 = .470606
• b)
• H_o: B = 0
• H₁: B <> 0


t = (b - B) / s_b = 1.12/.0470606 = 2.37991
Critical t = 2.069 ( two-tail with 23 df)
Thus reject the Null
Alternatively p-value = .02 (From Excel function tdist (2.37991, 23, 2) )
leading to the same conclusion

• c) B e { b +/- t_a* s _b}= 1.12 +/- 2.069 * 0.470606 = from 0.146478 to 2.09322.
To Top

---

• 12-37

 

 

Click for Excel output for part a) and part b
To Top


---

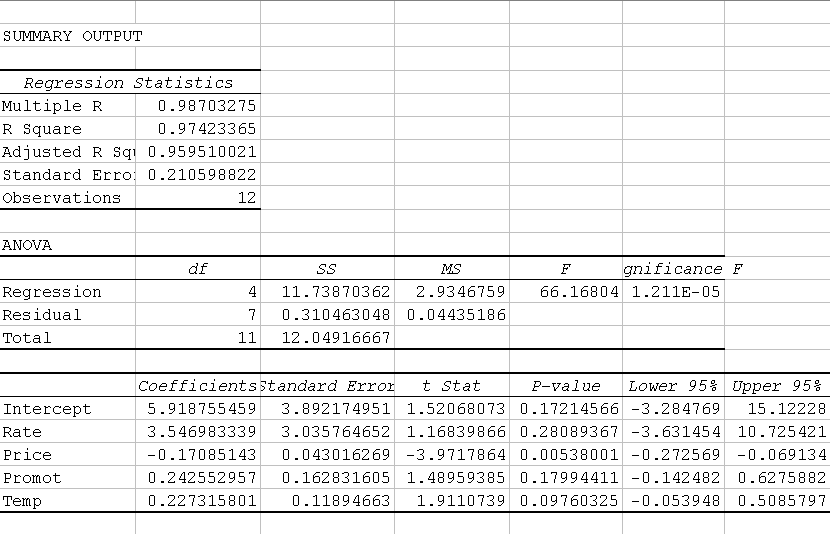
• 13-30
• 
• 
  
• Tourist = 5.918 + 3.547 * Rate -0.171 * Price + 0.243 * Promot + 0.227 * Temp
• b )
•  H_o: B₁ = 0
• H₁ : B₁ <> 0 ( Not zero)
• t - stat for b₁ =1.168398656

Critical t value for .10 level of significance ( .05 on either tail) with n-k-1 = 7 df is 1.895
Accept the null Hypothesis. Alternatively the p-value is 0.2809 leading to the same conclusion
 
• c)
•  H_o: B₃ = .2
• H₁ : B ₃ > .2 (..by more than..")
• t _stat = (0.242552957 - 0.2)/0.162831605= 0.261331069
• Since the critical t value with n - k - 1 = 7 df at 10% (two tail) is 1.895 we cannot reject the null hypothesis
• d) The 95% confidence interval for B₄ is {b ₄ +/- t_a* s_b4}

= 0.2273 +/- 2.365 * .1189 =
from -0.0539 to .5085
To Top

---