Freemark Abbey:

• At the outset there are two alternatives: (1) wait (W) for the storm to hit, if it will; (2) Harvest (H) now. If waited, the storm may or may not hit. If it hits the mold may or may not form grately affecting the revenue. If the storm hits and no mold forms, the eventual sugar level, which determines the quality of the wine and hence the revenue, is uncertain. Likewise the uncertainty  about the mold is quite important as it determines the difference between an exquisite wine versus a thin wine that the vinery may be unwilling to risk their reputation by selling it under company label.  This calls for another decision (if storm hits and the mold does not form): whether to sell the grapes in bulk (B) or make the thin wine and sell it under label (T). This decison however is different in that the EV will always favor making the wine since EV maximizes the current returns but cannot consider the long term marketing impact of selling the thin wine now. Thus this decision must be made outside the framework of the sequential decison based on monetary EV.
  
  
• 
  

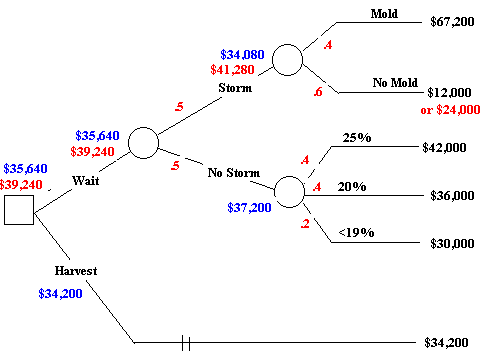
According to the above decision tree, solved on the assumption of (B), waiting for the storm has an EV of $35,640 versus (H) with an inferior EV of $34,200. Admittedly the diffrence is rather small (about 4.2% higher). If (T) is used the EV of (W) goes upto 39,240 which is substaintially more. However one has to cosider the negative long term effects of (T).
 
• If the probablity of the  mold is only 20% the (W)'s  EV drops to $30,120, making (H), the better alternative, not only in higher EV as well as lower risk.

• Again assuming (B) is used, EVPI (storm) can be calculated as follows: EV with prior knowledge of storm less EV without such knowledge. If it was known that the storm would hit the best alternative is (H) with expected revenue of $34,200 (versus $34,080); however if it were clear the storm would not hit then it is better to wait with EV of $37,200 (vs. $34,200). Thus with the prior knowledge the EV = .5 * 34,200 + .5 * 37200 =  $35,