Essentials of the Simplex Algorithm

In its bare essentials the simplex algorithm is a search method that systematically searches the corners of the feasible solution for an optimal one. It does that by the following procedure:

  1. Start at a convenient BFS (usually the origin)
  2. Test all the adjacent BFS for improvement in the OV
  3. IF none exists quit, the optimal solution has been found, otherwise continue
  4. Generate the adjacent BFS that improves the OV (PIVOT)
  5. Go to 2.

In the simplex algorithm each BFS is represented by a simplex table that contains information necessary (1)for the testing of the adjacent BFS for improvement; and (2) generating the simplex table that represents the adjacent BFS that offers improvement. Consider the problem: 


         MAX  2 X1 +   X2
  SUBJECT TO
         2)   3 X1 + 3 X2 <= 12
         3)     X1 + 3 X2 <=  6
Assume we add slacks SLK 2 and SLK 3 respectively to rows 2 and 3 to convert them into equalities. Thus we have 4 variables and 2 constraints. Remember that at every BFS only two of the four variables can be non-zero (basic). The simplex table corresponding to the origin (x1=0, x2=0, SLK 2=12, SLK 3=6) is given: 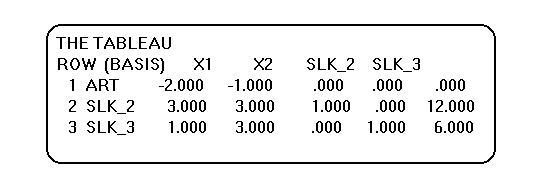The first row is the objective function. The column labeled (BASIS) always starts with ART, the name of the Objective function and lists the names of variables that are currently basic (SLK_2 and SLK_3 here). The first element in the last column is the current OV, the other entries contain the corresponding values of these basic variables. Currently OV is zero SLK_2 is 12 and SLK_3 is 6. (X1 and X2 are zero since they are not listed under BASIS). The first row under the variable names contain the "trial" reduced costs (RC). Remember what reduced cost measures: how much more attractive a variable has to become before it can be made positive (basic) . Using this definition we see that a negative RC for a non-basic (zero) variable indicates that the variable is too attractive not to be positive. At this point RC of X1 is -2. This signifies that the OV can be improved by making the value of X1 positive. However, since we are only interested in BFS, making X1 positive will require that one of the basic variables, SLK_2 or SLK_3, become non-basic (zero) to keep the number of positive variables at two. 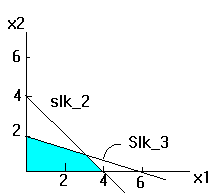If you look at the graph of feasible region you will notice that as X1 increases the solution (currently at the origin) will slide along the horizontal axis towards the two constraints and will reach the first constraint first, making its slack, SLK_2 zero.

This is a process called PIVOT (a math operation) which takes the simplex algorithm from one BFS to an adjacent one. The PIVOT that we described above will introduces X1 into the solution at a value of 4, making SLK_2 zero (nonbasic). The next BFS therefore will have X1 and SLK_3 as basic variables and SLK_2 and X2 as non-basic ones. The simplex table corresponding to this BFS is given below: This process of pivoting will continue until all reduced costs are non-negative at which time an optimal solution will have been found.