Welcome to PHYS 337/637

This course is a detailed introduction to variational methods in mechanics (Lagrangian and Hamiltonian formulations). It is highly theoretical in nature, developing an advanced formalism for dynamics that focuses on underlying symmetries and geometries. Specific reference to applications in astrophysics and cosmology will be made and transitional points to relativity and quantum mechanics will be given. The graduate 639 section is an excellent refresher for those preparing for the graduate qualifier (requires a few additional assignments). This course runs 1/2 a semester and is evaluated midterm (October).

Course Outline

1. I. 
   

2. 
   

3. Generalized coordinates, constraints and minimum coordinate sets
   

Virtual work and Maupertuis'/D’Alembert principles

Derivation of the Lagrangian

The resulting equations of motion

Lagrangian  multipliers

Exam 1

II.

1. Variational Calculus
   

Hamilton’s Principle

Action Integrals and the Lagrangian

III.
The Hamiltonian

Derivation of Hamilton's equations

Conservation principles

Phase Space and Global Behavior

Hamilton Jacobi  

Exam 2

Grades

The Class is made up of Lectures (which will be delivered on T/TH 12:30 to 1:40 with additional explanation and discussion), Weekly Homework, and Sectionals (problem solving sessions).  Grading assessments will provide a determination of:

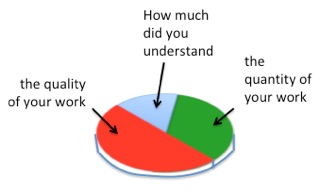
1) the quantity of work done by the student, (30% of grade)

2) the quality of work done by the student, (50% of grade)

3) the ability of the student to use concepts beyond what has already been presented to address unsuspected problems. (20% of grade) 

How you get Graded:

10%   Showing up to class and recitation, participating in discussions

20% Handing in the homework assignments with reasonable attempts to solve problems

50% Two, in class, quizzes.  They are weighted 25% each. The problems will be variations of the homework. Work the HW and understand each problem, you will do well on the quizzes.  

20% Challenge problems: take home portion of the quizzes. These problems are a little harder and add an additional 10% to the quiz. Generally, there will be 2 of these on each quiz.   

 

Narrative and Prerequisites

You have learned Newton’s laws and spent quite a bit of time applying them. So this class assumes a working knowledge of:

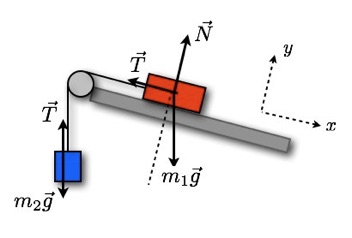
i.The freebody diagram

ii.Newton’s 3 main laws

iii.Kinetic and potential energy

iv.Collisions

v.*Extended bodies and Euler Angles

vi.Gravitational problems and Orbits

vii.*Harmonic and nonharmonic oscillations

The * topics are often missed, and they will be really important. So we will review these... 

The Newtonian approach makes use of the philosophy that abstraction of forces being applied to a body and the body then moving is a result of the forces. To be predictive, we have to be rather detailed about the nature of the forces: contact forces, gravitational forces, centripetal forces, and more. Newton’s laws then provide us with equations that describe a unique space-time path of each object, assuming we know the unique initial conditions of motion.

However in fields such as astrophysics, fluid dynamics, atmospheric science, etc, this can be a very difficult way to solve problems. Moreover, it isn’t very useful in approaching quantum mechanics.

The Text for the course is also quite helpful.  “A Student’s Guide to Lagrangians and Hamiltonians” by Patrick Hamill, Cambridge press.  You should read this each night and be familiar with the examples.