Double Integrals, Using Maple to approximate and find exact values.

The student calculus library contains a Doubleint command that can be used to display and evaluate double integrals.

> with(student);

> i:= Doubleint(exp(-x^2-y^2),x=0..1,y=0..1);

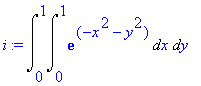
The standard value command can be used to try to get Maple to find the exact value of the double integral; Maple may not always be able to find the exact value or as in this case it may return an answer we don't comprehend.

> value(i);

In this and any case, we can use the evalf command, to obtain a numerical approximation of the integral.

> evalf(i);

If we trust that Maple has done the right thing (not always a good thing to do), the above answer should be the value of the double integral to ten decimal places (or at least nine). Now let us compute our own numerical approximations to the given double integral. Let us first partition the region of integration R = [0,1] x [0,1] into sixteen equally sized squares, and approximate choosing the sample point in each square from the lower right corner of the square. The area of each of the sixteen squares would then be 1/16.

> deltaA := 1/16;

The lower right corner points would then be

(1/4,0/4), (2/4,0/4), (3/4,0/4), (4/4,0/4)

(1/4,1/4), (2/4,1/4), (3/4,1/4), (4/4,1/4)

(1/4,2/4), (2/4,2/4), (3/4,2/4), (4/4,2/4)

(1/4,3/4), (2/4,3/4), (3/4,3/4), (4/4,3/4)

Note that in each, everything is fixed except that the numerator on the x runs from 1 to 4, and that in each column everything is fixed except that the numerator on the y runs form 0 to 3. We can program Maple to evaluate the given function at each of these points, and sum the results, but first we need to define our function.

> f:= (x,y) -> exp(-x^2-y^2);

Now we compute our sum. Notice that in the denominator of each x and y, I have put (4.) with a decimal point following it rather than just (4). This is a way of asking Maple to use a decimal approximation without using evalf . Note that we must multiply our sum by delta A to get our approximation.

> sum(sum(f(m/4.,n/4.),m=1..4),n=0..3)*deltaA;

The midpoint approximation using sixteen squares would evaluate the function at the following points. delta A would still have the same value.

(1/8,1/8), (3/8,1/8), (5/8,1/8), (7/8,1/8)

(1/8,3/8), (3/8,3/8), (5/8,3/8), (7/8,3/8)

(1/8,5/8), (3/8,5/8), (5/8,5/8), (7/8,5/8)

(1/8,7/8), (3/8,7/8), (5/8,7/8), (7/8,7/8)

Thus the midpoint approximation is given by

> sum(sum(f((2*m+1)/8.,(2*n+1)/8),m=0..3),n=0..3)*deltaA;

A nice graph of the volume represented by a double integral can be obtained by using plot3d with the axes=boxed and filled=true options.

> plot3d(f(x,y),x=0..1,y=0..1,axes=boxed,filled=true);