A Look at Some Infinite Series

The following output was generated using the partialsum command that

is found only in a special library that we call wfucalc . This library is not

part of the standard Maple load.

> with(wfucalc);

First we define the nth term of the sequence of terms

> a:=10/3^n;

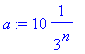
> partialsum(a,n=1..10);

In the table above, we see the decimal approximations of the sequence of terms in the second column, and the sequence of partial sums in the third column. Note that it appears that the sequence of terms is approaching 0 and the sequence of partial sums is approaching 5 although our conjectures would certainly require algebraic justification.

> b:=sin(n);

> partialsum(b,n=1..10);

In the above table the sequence of terms exhibits an oscillatory type behavior, and the sequence of partial sums is likewise oscillatory. Neither sequence appears to converge.

> c:=n/(n+1);

> partialsum(c,n=1..100,1,90);

In the above table, the sequence of terms begins to look like it may be converging to 1, and if further terms were examined the evidence would be stronger. Note that the sequence of partials sums, as a consequence, grows by about 1 at each step. Thus it would seem that the sequence of terms converges to 1, but the sequence of partial sums diverges to infinity. In other words, the series is divergent even though its sequence of terms is convergent.

> d:= 3/(n*(n-1));

> partialsum(d,n=4..100,1,90);

In the table above, the sequence of terms seems to be converging to 0, and while it is too early in the sequence to be sure, the sequence of partial sums is converging to 1 as we shall see later.

> e:=(-2/7)^(n-1);

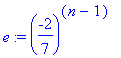
> partialsum(e,n=1..10);

In the above table, the sequence of terms appears to be converging to 0, and the sequence of partial sums seems to be converging to .7777777777... = 7/9

> f:=3^(-n)*8^(n+1);

> partialsum(f,n=1..10);

In the above table, the sequence of terms seems to be diverging to infinity, and the sequence of terms is likewise diverging to infinity.