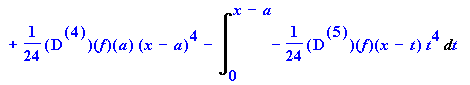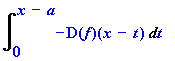
Taylor's Formula

Derivation of Taylor's formula using integration by parts. We will need the student library; a colon is used instead of a semicolon to suppress printing of all the function names.

> with(student):

The value of the following integral will be used to get things started.

> Int(diff(f(x-t),t),t=0..x-a);

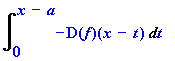
> value(%);

Rewrite the above by solving for f(x).

> f(x) = f(a) - Int (diff(f(x-t),t),t=0..x-a);

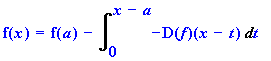
Now integrate by parts choosing u to be the derivative in the integrand.

> intparts(%,diff(f(x-t),t));

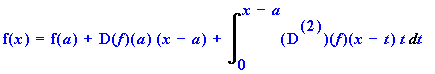
Integrate by parts, again choosing u to be the derivative in the integrand.

> intparts(%,diff(f(x-t),t$2));

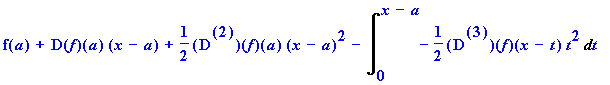
And, again.

> intparts(%,diff(f(x-t),t$3));

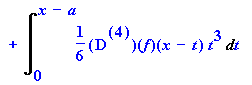
One more time!

> intparts(%,diff(f(x-t),t$4));