Taylor Polynomials

The standard Maple command taylor can be used to generate the first few terms of the Taylor's

or Maclaurin's series for a function. Three parameters are required. The first is an expression

for the value of the function, the second is x=0 for a Maclaurin's series or x=a if a Taylor's

series in powers of (x-a) is desired, and the third is the number of terms desired or one larger

than the highest power required (because the constant term is an extra term).

> taylor(sin(x),x=0,11);

> taylor(sin(x),x=Pi/2,9);

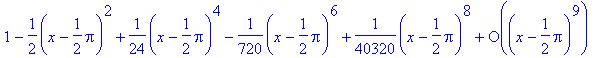
The last term is called a Big Oh term, and represents the fact that the tail end of the series is less than

some constant times the absolute value of the power inside the parentheses following the Big Oh

symbol. The output of the taylor command can be used to see as many terms of the Taylor's series as desired, but it is not useful for evaluation or graphing. The taylorfunction command in the wfucalc library may be used for evaluating and graphing Taylor polynomials of a function. For example the third, fifth, and seventh degree Taylor polynomials about x=0 for sin(x) can be defined as follows:

> with(wfucalc);

> p3:=taylorfunction(sin(x),x=0,4);

> p5:=taylorfunction(sin(x),x=0,6);

> p7:=taylorfunction(sin(x),x=0,8);

Now compare the approximations these polynomials (or partial sums) give to the actual value of sin(1).

Note that p3 gives only about 1 decimal accuracy, while p5 gives about 2 or 3 decimal accuracy, and p7 gives about 4 decimal accuracy.

> evalf([sin(1),p3(1),p5(1),p7(1)]);

Now let's compare the graphs of sin(x) with each of these Taylor polynomials.

> plot([sin(x),p3(x),p5(x),p7(x)],x=-4..4,y=-4..4,color=[red,green,blue, yellow]);

Next, we look at the Taylor polynomials for sin(x) about x =Pi/2, and compare their graphs with the graph of sin(x) when x is near Pi/2.

> q2:=taylorfunction(sin(x),x=Pi/2,3);

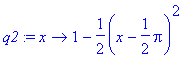
> q4:=taylorfunction(sin(x),x=Pi/2,5);

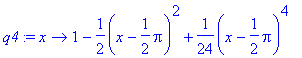
> q6:=taylorfunction(sin(x),x=Pi/2,7);

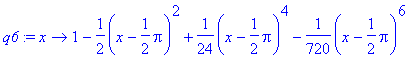
> plot([sin(x),q2(x),q4(x),q6(x)],x=-2..5,color=[red,green,blue,yellow]);

>