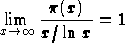be the
number of primes less than or equal to x; Gauss had guessed that
(this is the prime number theorem).
Chebyshev showed that
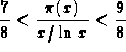together with the fact that the limit must be 1, if it exists.
Pafnuty Lvovich Chebyshev
The Russian mathematician Chebyshev made important
contributions to number theory, probability theory, and function approximation
using orthogonal polynomials. Although younger than Lobachevsky, Chebyshev
was considered a rival. While Lobachchevsky was isolated at Kazan, Chebyshev
spent his career at St. Petersberg, where Euler
spent much of his life; Chebyshev is considered the founder of the St.
Petersberg school of mathematics, and his mathematical descendants
include Markov, Lyapunov, and Kolmogorov. His work was well-known in europe
since he published in european journals and made several extended trips
to european mathematical centers; he was eventually elected to many
foreign memberships including the Royal Society and France's Academy
of Sciences. His mathematical legacy includes Chebyshev polynomials in
approximation theory, the law of large numbers in probability theory, and
almost a proof of the prime number theorem. Let be the
number of primes less than or equal to x; Gauss had guessed that
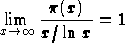(this is the prime number theorem).
Chebyshev showed that
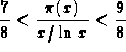together with the fact that the limit must be 1, if it exists.
 |
 |
| P.L. Chebyshev(1821-1894) | P.L. Chebyshev(1821-1894) |
| Russia (1946), No. 1050 | Russia (1946), No. 1050 |
|
| P. L. Chebyshev (1821-1894) |
| Russia (1946), No. 1051 |