The Theory Behind Chinese Music
First, listen to the
Equal Tempered tuning used to play a scale. This is the scale you will hear on a properly tuned piano.
Now, listen to one of the many
Chinese tunings used to play a similar scale. Unless you have perfect pitch, you might not be able to tell the difference without a better
musical context. Later on in this discussion, you will be given an opportunity to hear identical melodies played in Equal Tempered and Chinese 12 Lyu tunings.
(By "tuning" I mean a rule that one uses to determine how to tune the strings of an instrument such as a harp so that it will play the
frequencies that it is supposed to play.) Because of the notes coming in a musical sequence, and because frequently several notes are played
at the same time, you will be better able to hear the differences among the various tunings.
Before we can talk about the Chinese musical scales, it may be
helpful to review some things about our own music and what we
consider to be harmonious. The original Chinese musical theory
was probably developed by making rules for the lengths of a set of
bamboo tubes that were made to be blown, perhaps in the way that
people now blow over the ends of bottles to make a musical note.
It will be easier to explain things in terms of stringed instruments.
Let's start with a long narrow piece of wood that is over a meter
long. At the left end (unshown) we will put tuning pegs, and
at the right end we will put a resonating chamber. But for right
now we are just concerned with what will be analogous to the
long neck of a guitar with its frets. The vibrating part of our
strings will be 100 cm. long.

(Click the above image to hear the open string play.)
Or click
here .
The easiest way to get harmonious singing is for everyone to
sing the same note. But people sing in different registers, some
high and some low. We say that they are singing the same note,
but actually the frequencies they sing are found by doubling
some fundamental frequency, doubling it again, and so on. We
say that these people are singing an octave, or octaves, apart.
Let's put a metal fret at the midpoint of the actively vibrating
part of our string. If you halve the length of a string (and
don't change its tension), then you double its frequency.

(Click the fretboard image to hear the fundamental frequency and the frequency an octave higher.) Or click
here .
If we were actually to build this instrument, we could provide
several strings. We could set them all to A=440, stop one string
with our finger at the middle fret, and play that one and an
unstopped string together. We would hear frequencies of 440
hertz and 880 hertz together. We could even add another fret a
quarter of the way from the right end, giving us 1760 hertz.

(Click the keyboard image to hear the fundamental frequency, the frequency an octave higher, and the frequency two octaves higher.) Or click
here .
If we multiply the fundamental frequency (in this case 440 hertz)
by an even number we will find that the high frequency waves
fit exactly within the envelope created by the fundamental frequency.
To human being, and apparently to many of our animal friends, such
sounds are more pleasant. To experience a counter-example, try
striking two adjacent keys on a piano, or playing two adjacent
holes on a harmonica. Or, try listening to this recording of two guitar strings
tuned so as to produce an unpleasant interaction.
An
unpleasant chord.
When two sound waves interfere, part of the time they augment each other, but part of the
time one sound wave is trying to do the opposite of the other sound wave. The result is
that the sound you hear comes and goes very rapidly. You will hear a kind of "wah, wah,
wah, wah, wah" as a result. If you have a piano available, you can try various combinations
for yourself. Playing four notes together, A, A an octave higher, F, and F an octave higher
may produce some interesting results. You can also listen to a "wav" file below. This
example gives the high F first, to demonstrate the highest note that is actually played in the
second part. When the second part comes on, you may be able to hear two interesting things.
There is a "wah-wah" fluctuation that occurs about every half second, and has a low, buzzy
quality. There is also a high frequency tone, an octave higher than the single reference tone at
the beginning of the recording that has a pronounced warble.
Hear the high
"ghost" instrument.
In the graph drawn below, the grayed-in areas are the parts where the two sound waves
interfere. You would hear the sound "drop out" at this point.
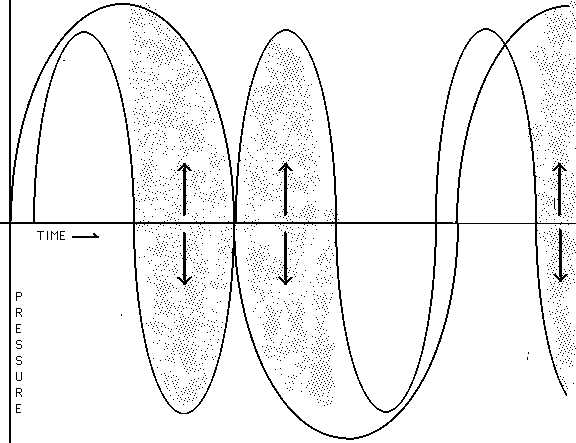
We don't want an irritating fire siren type sound.
So let's add a second fret that will give us harmony. We started with 100 cm. divided by
1. 100 cm. / 1 = 100 cm. Then we put down one fret in the middle.
That's 100 cm./2 = 50 cm. and it gave us the octave. Now we will try 100 cm./3 = 33.33...3
cm. But putting a fret there would be too near the right end
of the string. It would be an octave higher than we want. So
we will double that length (making it an octave lower than it
was). Then we have (100 cm. /3)*2=66.66...6 cm.
We found out by experiment that halving the length of a string
doubles its frequency. The general relationship is given by
the equation:
L1/L2 = F2/F1 so F2= (L1/L2)*F1.
100/50 = F2/440 so F2=(100/50)*440=2*440=880
We could divide the string into thirds, too:
100/66.66...6=F2/440 so F2=(100/66.66...6)*440=((100*3)/(2*100))*440=3*220=660
In this scale, 660 hertz is E.

(Click the picture to hear this note play.)
Or click
here .
4/3 yields a D. The string length
is about 75 cm. and the frequency is 586.6..6 hertz.

(Click the picture to hear this note play.)
Or clickHERE
6/5 produces a string length of 83 1/3 cm. and a frequency of 528 hertz. That is a C.

(Click the picture to hear this note play.)
Or click here .
So let's try 5/4. Following the mathematical steps shown above,
that will give us a fret at the 80 cm. mark (20 cm. from the
tuning pegs), and a frequency of 550, which is C#.

(Click the picture to hear this note play.)
Or click here .
5/3 yields a string length of 60 cm. and a frequency of
733.3..3 hertz. That's an F#.

(Click the picture to hear this note play.)
Or click here .
The next multiple of the fundamental frequency we could try is
7. 7/4 gives us a frequency of 770 hertz and tells us to
set a fret so that we can use a string length of about 57.1 cm.
That will give us a G.

(Click the picture to hear this note play.)
Or click here .
7/5 yields about 71.43 cm and 616 hertz for an D#.

(Click the picture to hear this note play.)
Or click here .
8/5 yields yields 62.5 cm and 704 hertz. That gives us an F.

(Click the picture to hear this note play.)
Or click here .
9 is the next multiplier, and it yields a frequency of 495 hertz
and a string length of about 88.9 cm. That's a B.

(Click the picture to hear this note play.)
Or click here .
15 yields a string 53 1/3 cm. long and a frequency of 825, a
G#.

(Click the picture to hear this note play.)
Or click here .
16/15 yields a string 93.75 cm. long and a frequency of 469 1/3 hertz, an A#.

(Click the picture to hear this note play.)
Or click here .
Now let's hear the diatonic scale (the one that goes "do, re, mi...") in that tuning.
Click here .
If you have perfect pitch, or even just perfect relative pitch,
you may have been troubled by the feeling that certain notes
on various musical instruments sound out of tune. And yet, all
the musical instruments have the same frequencies. It's not the
fault of your ears. It's because we play a tempered scale --
a scale that slightly detunes certain notes so that when a piece
of music is transposed to another key it still sounds
to us as though it is in key.
Tables at the end of this article will show differences that
cause problems when transposing keys in untempered scales, and
they will also show how the Chinese gamut of frequencies differs
from an untempered Western scale and the tempered Western scale.
Now let's put down frets according to the Chinese method. This
method has an ancient history, and was first written about in
the Lyu Shi Chun-qiu, a text produced by the "think tank"
of a late Zhou dynasty figure around 239 B.C., and the Guan Zi, a syncretic
text attributed to a very early figure, Guan Zhong, who died in 644
B.C. The book may have been compiled in the late fourth century B.C.,
but may also contain materials going back to the historical Guan Zhong's time.
The Chinese rule is very simple: Take 2/3 of the length of the
open string, and put down a fret there. Then take 4/3 of that
second length and put down a fret there. The third step is to
take 2/3 of the last length, then 4/3, and so forth. Let's see
how that works.

(Click the picture to hear this note play. It is the open string, which will
be set to 440 for ease of comparison, and called by the Chinese name, Huang Zhong.)
Or click here .
The first step is to put down a fret that will leave 2/3 of
the whole string free to vibrate. If the open string is tuned
to 400 hertz, then stopping a fret at the 2/3 mark will provide
660 hertz. This note is called Lin Zhong in Chinese.

(Click the picture to hear this note play.)
Or click here .
The second step is to put a fret at a point 4/3 of the stopped
length of the string just determined. That fret will provide
495 hertz. It is called Da Cu.

The third step puts a fret at a point 2/3 of the stopped length we just created,
and it provides 742.50 hertz. (Nan Lyu)

Step four uses 4/3 and provides about 556.88 hertz. (Gu Xian)

(Click the picture to hear this note play.)
Or click here .
Step five uses 2/3 and provides about 835.31 hertz. (Ying Zhong)

(Click the picture to hear this note play.)
Or click here .
Step six uses 4/3 and provides about 626.48 hertz. (Rui Bin)

(Click the picture to hear this note play.)
Or click here .
Step seven uses 4/3 and provides about 469.86 hertz. (Da Lyu) (If we'd used 2/3, we'd have gone an octave too high.)

(Click the picture to hear this note play.)
Or click here .
Step eight uses 2/3 and provides about 704.79 hertz. (Yi Ze)

(Click the picture to hear this note play.)
Or click here .
Step nine uses 4/3 and provides about 528.60 hertz. (Jia Zhong)

(Click the picture to hear this note play.)
Or click here .
Step ten uses 2/3 and provides about 792.89 hertz. (Wu Yi)

(Click the picture to hear this note play.)
Or click here .
Step eleven uses 4/3 and provides about 594.67 hertz. (Zhong Lyu)

(Click the picture to hear this note play.)
Or click here .
Step twelve uses 2/3 and provides about 892 hertz. Note that
the true octave is at 880 hertz. Using this system would never
permit derivation of the true octave. But the method used here
continually divides frequencies by two (or multiplies string lengths
by two) to make a gamut all the notes of which fall within one octave,
so it is clear that the early Chinese had a definite idea of how to define
and use the octave. The values derived in this twelfth step are not
used in normal musical practice.

(Click the picture to hear this note play.)
The following is a comparison of the fret placement by the Chinese
method (the lower set of frets) and by the Western method detailed above.

If somebody took an ordinary guitar and redid the frets as a practical joke,
the guitarist who tried to play a tune would surely feel that something was wrong.
If a few more frets were put into the diagram of western frets to provide for some
of the sharps and flats, then things would look a little better. But remember that
the way the frets were originally set was according to what would make harmonious
chords regardless of what key a song may be played in. If somebody moves
those frets more than a tiny bit, then harmony will be replaced by discord.
On the other hand, if a musician has an instrument like the bagpipe that is not very
much like other instruments, then the only thing to do is to learn what can be done
with that instrument that is musically interesting and pleasing. And any gamut that
can be produced will present a different set of possibilities and difficulties.
Traditional Chinese music uses a gamut of frequencies that are guaranteed to provide
some level of discord in certain combinations that would sound more harmonious
in the western musical tuning described above or even in the Equal Tempered tuning.
But sometimes people like a little discord for the sake of spice, and a piece of music
that is composed with the Chinese system in mind can sound more brilliant and endearing
than the same piece played in the Equal Tempered tuning -- because most notes in that
system are deliberately flatted as a way to provide a compromise tuning that will tolerate
transposition from one key to another.
Most of us grow up using the tempered scale which you can produce for yourself on any well-tuned
piano. But that scale is mathematically rather sophisticated. (It involves complications involving the
twelfth root of two.) Before that scale was invented, some less sophisticated scales were produced.
Two of them are shown for comparison in the chart below.
One of the reasons for inventing mathematically defined scales was to facilitate the creation of musical
instruments that permit transposing from key to key. The advantage is that one can play in many keys
without having many sets of musical instruments or constantly retuning one set of instruments. The disadvantage
is that they are all compromises. They are all slightly out of tune and produce some degree of discord.
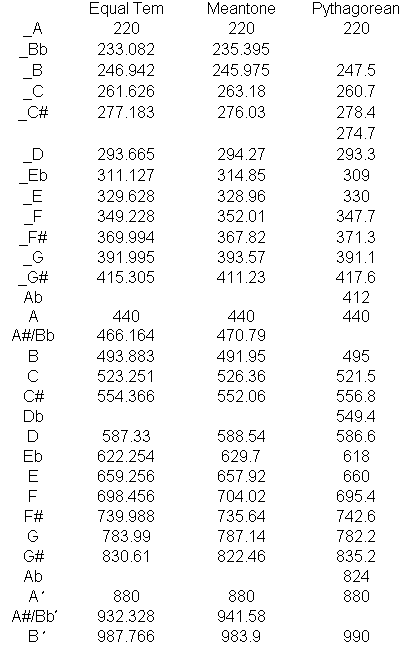
Western musicians avoid discord by striking compromises. The present Western attitude seems to be that if transposing a
song from the key of C to the key of E makes it sound different, makes some notes sound flat or some notes sound
sharp, then that is a problem that needs to be solved. The Chinese knew about the tempered scale even before it was
invented in the West, but they chose not to use it. They seem to have decided to put the differences to good use. If the
equivalent of "do mi mi, mi so so" sounds different in the equivalent of their key of C and their key of E, then that is a
useful thing because the feeling that goes along with those sounds is different. That is similar, but much richer,
than our practice of having some songs written in major keys and other songs written in minor keys. In our own musical
tradition, there was originally a richer musical palette that included a gamut of frequencies that was not our current
equal tempered gamut, and several different modes or selections of notes to play on from within a gamut of frequencies,
and the emotional characteristics of these gamuts and modes was also a staple of formal musical instruction.
The Chinese system is based on the mathematical method of working back and forth by taking 3/2 of a base frequency,
3/4 of the frequency so produced, and so forth. Once a series of 12 frequencies is produced, they use each of those 12
frequencies as the fundamental frequency for a new scale. The result is 144 frequencies. (It turns out that there are quite
a few duplications.) That gives the Chinese musician quite a large set of frequencies to play music with.
If the musical intervals between notes were exactly equal, then the numbers along any diagonal that rises from left to right should
be the same. But, in fact, the intervals are not equal, and the numbers along those diagonals are not always equal.
Note that the bottom line turns out not to be a true octave above the top line. Each of the numbers calculated is somewhat higher
than the octave.




























