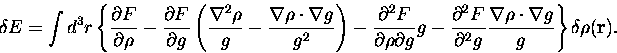Next: About this document ...
September 9, 1998
PHY 711 - Problem Set # 6
Consider an integral of the form:
![\begin{displaymath}
E = \int \: d^3r \: F[\rho({\bf{r}}),g({\bf{r}})],
\end{displaymath}](img1.gif)
where 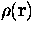 is a function of position in three dimensions, and
is a function of position in three dimensions, and 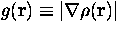 . Show that the functional variation of E with respect to
. Show that the functional variation of E with respect to 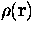 is given by:
is given by:
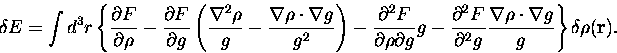
natalie holzwarth
9/9/1998
![]()