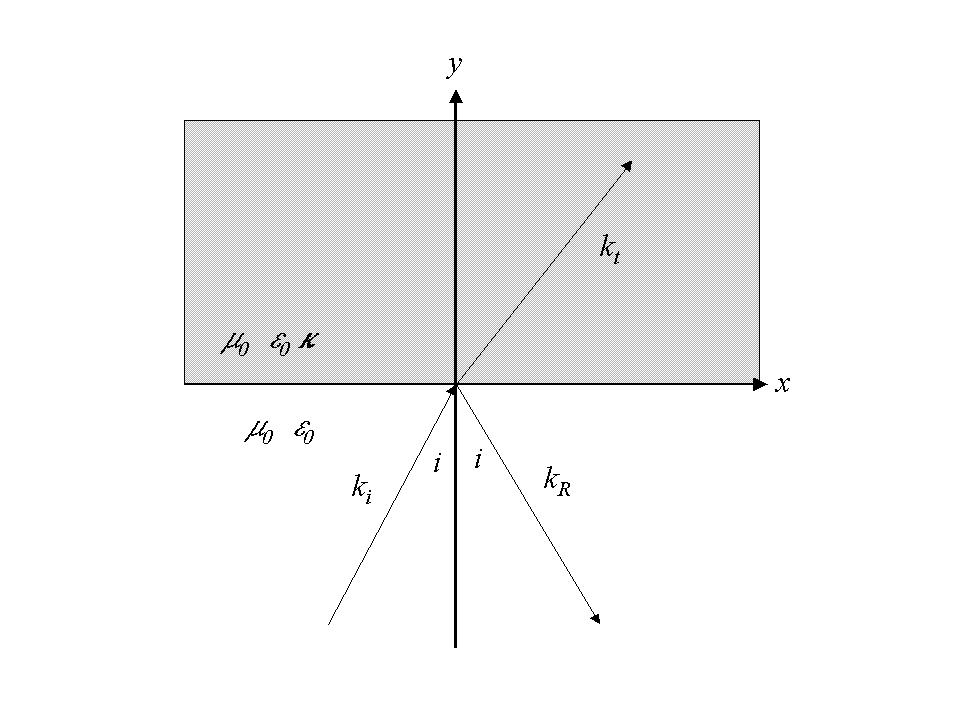
 Consider the problem of determining the reflectance from an
isotropic medium as shown above. For simplicity, we will assume
that the dielectric tensor for the medium is diagonal and is
given by:
Consider the problem of determining the reflectance from an
isotropic medium as shown above. For simplicity, we will assume
that the dielectric tensor for the medium is diagonal and is
given by:
Figure
 Consider the problem of determining the reflectance from an
isotropic medium as shown above. For simplicity, we will assume
that the dielectric tensor for the medium is diagonal and is
given by:
Consider the problem of determining the reflectance from an
isotropic medium as shown above. For simplicity, we will assume
that the dielectric tensor for the medium is diagonal and is
given by:
| (1) |
| (2) |
| (3) |
| ||||||||||
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Below we consider two different polarizations for the electric field.
| (10) |
| |||||||||||||
| (12) |
| (13) |
| (14) |
| (15) |
| |||||||||||||||||
| (17) |
This result reduces to Eq. 7.41 in Jackson for the isotropic case.