Jan 29, 2001

Notes for Lecture Notes for Lecture #5

Methods for solving Poisson equation

There are are large number of tools for solving the Poisson and Laplace equations:

  1. Green's function methods:
    F(r) = 1
    4pe0
    		 ó
    õ

    V 
    		 d3r¢ r(r¢) G(r,r¢) + 1
    4p
    		 ó
    õ

    S 
    		 é
    ê
    ë     		G(r,r¢) F
    n¢
    		 - F(r¢) G(r,r¢)
    n¢
    		 ù
    ú
    û     		da¢.
    		(1)
  2. Complete function expansions; Fourier series, etc.
  3. Variational methods
  4. Grid based methods

Introduction to grid-based methods

The basis for most grid-based methods is the Taylor's expansion:

F(r + u ) = F(r) + u·Ñ F(r) + 1
2!
 (u·Ñ)2 F(r) + 1
3!
 (u·Ñ)3 F(r) + 1
4!
 (u·Ñ)4 F(r) + ¼.
(2)

We will work out some explicit formulae for a 2-dimensional regular grid with h denoting the step length. For the 2-dimensional Poisson equation we have

æ
ç
è 		2
x2
 + 2
y2
 ö
÷
ø 		F(x,y) = - r(x,y)
e0
 .
(3)
We note that a sum of 4 surrounding edge values gives:
SA º
F(x+h,y) + F(x-h,y) + F(x,y+h) + F(x,y-h)
(4)
=
4F(x,y) + h2 æ
ç
è 		2
x2
 + 2
y2
 ö
÷
ø 		F(x,y) + h4
12
 æ
ç
è 		4
x4
 + 4
y4
 ö
÷
ø 		F(x,y) + (h6¼).
Similarly, a sum of 4 surrounding corner values gives:
SB º
F(x+h,y+h) + F(x-h,y+h) + F(x+h,y-h) +F(x-h,y-h)
(5)
=
4F(x,y) + 2h2 æ
ç
è 		2
x2
 + 2
y2
 ö
÷
ø 		F(x,y) + h4
6
 æ
ç
è 		4
x4
 + 4
y4
 + 6 2
x2
 2
y2
 ö
÷
ø 		F(x,y) +(h6¼).
We note that we can combine these two results into the relation
SA + 1
4
 SB = 5 F(x,y) + 3h2
2
 Ñ2F(x,y)+ h4
8
 Ñ2 Ñ2 F(x,y) + (h6¼).
(6)
This result can be written in the form;
F(x,y) - 1
5
 SA - 1
20
 SB = 3h2
10 e0
 r(x,y) + h4
40 e0
 Ñ2 r(x,y).
(7)
In general, the right hand side of this equation is known, and most of the left hand side of the equation, except for the boundary values are unknown. It can be used to develop a set of linear equations for the values of F(x,y) on the grid points.

For example, consider a solution to the Laplace equation in the square region 0 £ x £ a, 0 £ y £ a which F(x,0) = F(0,y) = F(a,y) = 0 and F(x,a) = V0. We will first analyze this system with a mesh of 9 points. In this case, f5 º F(a/2,a/2) is unknown, while f1 = f2 = f3 = 1 and f4 = f6 = f7 = f8 = f9 = 0.

Figure 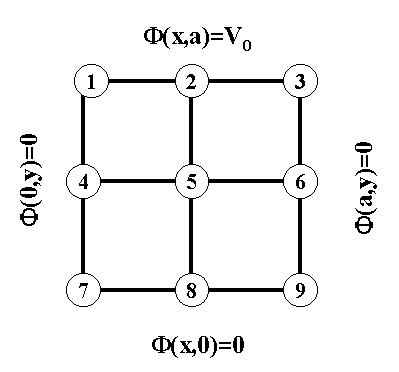For this example, Eq. 7 states

f5 = 1
5
 (f2+f4+f6+f8)+ 1
20
 (f1+f3+f7+f9) = 3
10
 V0.
(8)
This results is within 20% of the exact answer of F(a/2,a/2) = 0.25 V0. If analyze this same system with the next more accurate grid, using the symmetry of the system F(x,y) = F(a-x,y), we have now 6 unknown values {f5,f6,f8,f9,f11, f12} and boundary values f1 = f2 = f3 = 1 and f4 = f7 = f10 = f13 = f14 = f15 = 0.

Figure 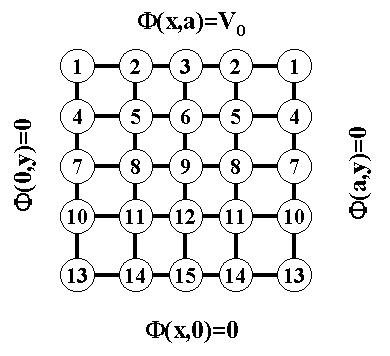This results in the following relations between the grid points:

f5- 1
5
 (f2+f4+f6+f8) - 1
20
 (f1+f3+f7+f9) = 0,
(9)
f6- 1
5
 (f3+f5+f5+f9) - 1
20
 (f2+f2+f8+f8) = 0,
(10)
f8- 1
5
 (f5+f7f9+f11) - 1
20
 (f4+f6+f10+f12) = 0,
(11)
f9- 1
5
 (f6+f8+f8+f12) - 1
20
 (f5+f5+f11+f11) = 0,
(12)
f11- 1
5
 (f8+f10+f12+f14) - 1
20
 (f7+f9+f13+f15) = 0,
(13)
f12- 1
5
 (f9+f11+f11+f15) - 1
20
 (f8+f8+f14+f14) = 0.
(14)
These equations can be cast into the form of a matrix problem which can be easily solved using Maple:
















(
1
-1/5
-1/5
-1/20
0
0
-2/5
1
-1/10
-1/5
0
0
-1/5
-1/20
1
-1/5
-1/5
-1/20
-1/10
-1/5
-2/5
1
-1/10
-1/5
0
0
-1/5
-1/20
1
-1/5
0
0
-1/10
-1/5
-2/5
1\end array
)
f5
f6
f8
f9
f11
f12 \end array
) =
3/10
3/10
0
0
0
0\end array
) V0. (15)