Physics 266 Lab I

1) Two logs, each of weight W, lie in a trough with vertical walls in such a way that when viewed end-on the line between their centers makes an angle q with the horizontal. The magnitude of the forces on the bottom log due to the top log, the bottom of the trough, and one wall on the trough are F₁₂, F_1b, and F_1w, respectively. Similarly the forces on the top log due to the bottom one and the other wall are F₂₁ and F_2w. Since F₁₂ = F₂₁, three equations for static equilibrium are

-F₁₂ cos(q) + F_1w = 0

F_1b - W - F₁₂ sin(q) = 0

F₁₂ cos(q) - F_2w = 0

Assuming that all frictional forces are negligible. Find a fourth equation and use Maple to

1. Find the magnitude of the forces F₁₂, F_1b, F_1w, and F_2w. That is find the forces in terms of W and q.
2. Check the solutions



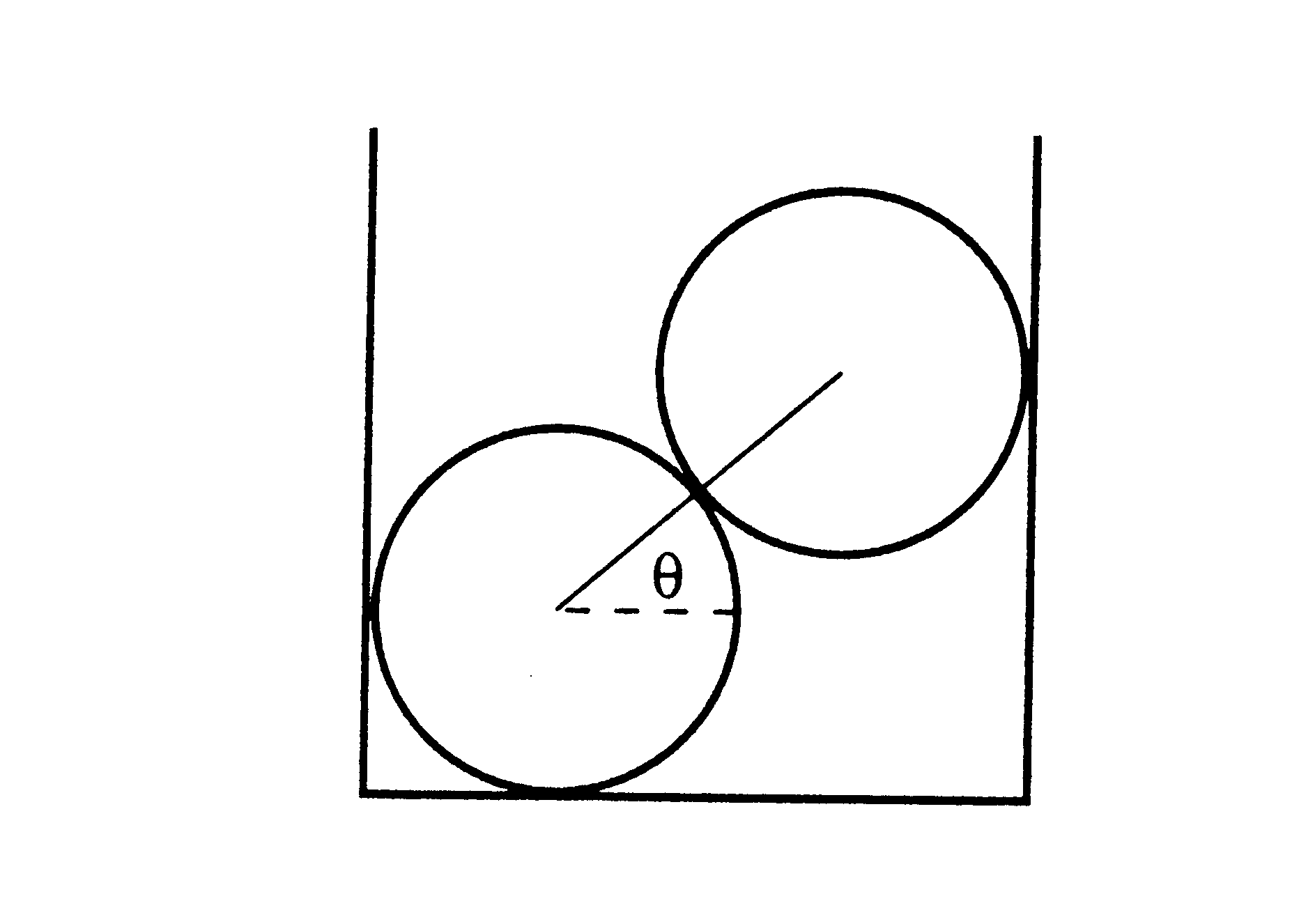
2)Consider the binding of nitric oxide to methemoglobin



Let K be the dissociation equilibrium constant so that

K = [NO][MetHb]/[MetHb-NO].

Take K to be 250 micromolar, expressing all values in micromolar, solve for how much free NO and MetHb are present when the initial concentrations of NO and MetHb are 30 and 1000 microlmolar.