Lab III Simple Mechanics and Graphing

I. Look up "plot" or Plottng Guide in Maple help could go under Visulaization

II. Do the following problem:

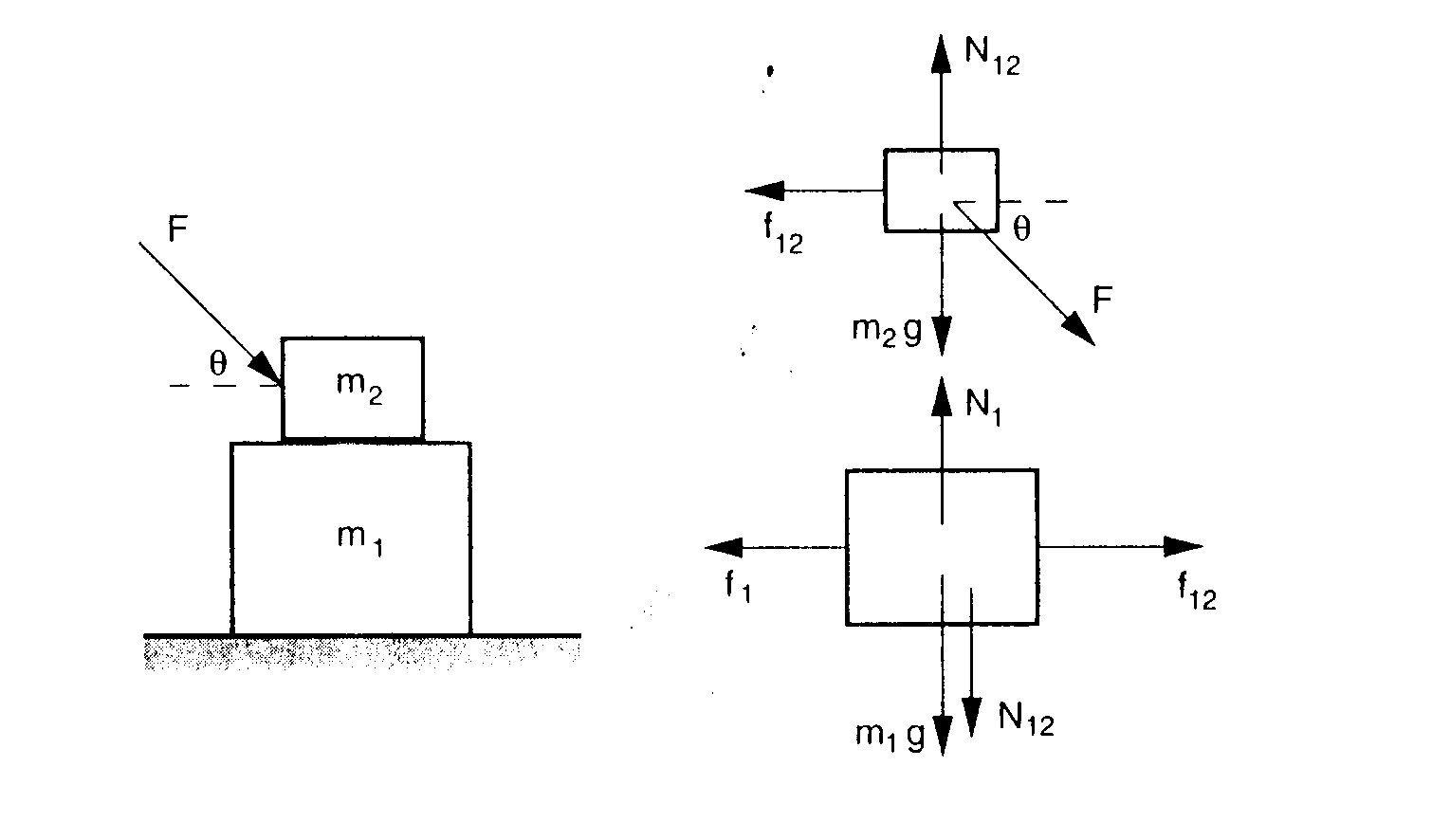
Two boxes are stacked on a table as shown below. A force F is applied to m₂ at an angle q with respect to the horizontal. Assume the boxes are moving to the right and the coefficient of kinetic friction between the mass and the table is u, and the coefficient of static friction between the boxes is sufficiently large so that they do not slide with respect to each other. Your goal is to

(a) Using Maple, show the general expression for the force, F, in terms of m₁, m₂, m, and g where the acceleration becomes zero is F₀ = (u g (m₁ + m₂))/(cos(q) - u sin(q)) [provided it is positive]. [You will have to derive equations of motion from Newton's second law].

Hints The accelerations of the masses are the same. f1 = u N₁. Solve the four equations using sol := solve({eq1, eq2, eq3, eq4}, {a, N1, N12, f12}); After you have solved the 4 equations, assign the solution using assign(sol). Then solve for the force, F, using solve(a=0,F).

(b) Find the critical angle q_c such that when q > q_c the force F is no longer able to maintain the systems motion to the right, no matter how big F is. From your expression in part (a), note that when q = q_c, F must become infinitely large. What is the acceleration when q = q_c? How does it compare to the acceleration when F is zero?

HintsTo obtain the critical angle, solve the denominator from your expression for (a) for zero. The answer will be in terms of u. To get the acceleration when F is applied at the critical angle, first define the acceleration as a function of F and theta using the statement, A := unapply(a,F,theta).

(c) Let m₁= 3 kg, m₂= 1 kg, u = 0.8 and g = 9.8 m/s². Define the acceleration as a function of q and F. Plot the acceleration when F = 10 N when q goes from 0 to p/2. Repeat this for when F = 100N. Then make a 3D plot of the acceleration vs. q going from 0 to p/2 and F going from 10 to 1000 N. Can you get q_c from the plot?

Note: You can do these plots two ways. First use plot(A(10,theta), theta=0..Pi/2) for example or (for the 3D plot) plot3d(A(F,theta), F = 10 .. 1000, theta = 0 .. Pi/2, axes=NORMAL);. Second, you can recall A(10,theta) and then right click on it to plot. After you get the plot using this second method, you can fix the axes range and anything else you want.