Lab VI Simple Harmonic Motion

Continued

III (a) Let the harmonic oscillator of IIa (characterized by w₀ and β) now be driven by an external force, F = F₀sin(wt). Use Maple to solve the differential equation describing the motion of the mass. Simplify the result by collecting factors that involve F₀ and assign this to x(t). Point out the complementary (general) and particular parts of the solution.

Hints The equation can be written:

eq := diff(x(t),t,t) + 2*beta*diff(x(t),t) + omega0^2*x(t) = Fo/m*(sin(omega*t));

Solve the equation using dsolve (that is, use sol := dsolve(eq,x(t)): and then use

assign(collect(sol,Fo,factor)): x(t);

Note that in this lab (especially) using a colon instead of a semicolon will help conserve screen space.

(b) Your general solution should have two arbitrary constants. Repeat part (a) only this time solve the differential equation with initial positions and velocities, x0 and v0.

Hints: Restart. Then define the same equation as above only this time when soving it use

sol := dsolve({eq,x(0)=x0, D(x)(0)=v0},x(t)):

instead of sol := dsolve(eq,x(t)): that you used in part a. You should still use the same assign(collect(sol,Fo,factor)): x(t): term after.

(c) Define the velocity, v, kinetic energy, K, and potential energy U(in terms of w₀). Define the total energy, En, as a function of w and time; use the real part of K+U to prevent small calculated imaginary parts in round off error. Assign: m=1, w₀ =1, F₀ = 1, β = 1/10, x0 = 0 and v0=0 (Remember to use :=). Plot the total energy for w = 0.5, 0.9, and 1 for time, t = 0 to 100. What value of w absorbs the most energy? To examine this further, make a 3D plot of the energy for t from 0 to 30 and w from 0 to 2 (to see the axes add the command axes=frame).

Hints Thus you will define v:=diff(x(t),t): K:=1/2*m*v^2: U:=1/2*m*(omega0*x(t))^2: and En := unapply(Re(K+U),omega,t):

The basic form a 1D plot would be (for example) plot(En(0.5,t), t = 0..100);

The 3D plot would be written plot3d(En(omega,t),t=0..30,omega=0..2,axes=frame);

(d) Examine the power absorbed by the oscillator to better study the resonance phenomenon. The power absorbed over a period, T =2π/w, will be the integral of the external force times the velocity of the mass with respect to time. The average power will be the power over the period. Define P0, the initial average power, as a function of beta (you should unassign beta) and the average power as the 1/T times the integral from t = 0 to t =T (define the period T = 2 π /w) of v*F. Define Pss as a function of beta and omega as the 1/T times the integral from t = 10/b to t =T+ 10/b of v*F (this is the steady state average power). Plot P0 and Pss as w goes from 0 to 4 with β = 0.1. What can you say about resonance at early times? Explore the effect of damping on resonance by plotting Pss as w goes from 0 to 4 with β = 0.1, 0.25, and .5.

Hints: Here are some commands that may be useful (in other words this will work):

beta:='beta':

T:=2*Pi/omega:

int(v*Fo*sin(omega*t),t=0..t0+T)/T:

AvgPower:=unapply(%,t0,beta,omega):

P0:=(beta,omega) -> Re(AvgPower(0,beta, omega)):

Pss:=(beta,omega) -> Re(AvgPower(10/beta,beta, omega)):

Then you can plot both together as plot({P0(.1,omega),Pss(.1,omega)},omega=0..4); or plot separately. To explore the effect of damping, use plot({Pss(.1,omega),Pss(.25,omega), Pss(.5,omega)},omega=0..4);

IV. Impulse driven harmonic oscillator. Now let the external force be a series of impulses

,

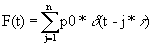where d represents the dirac delta function (Dirac in Maple) and t is the time interval between consecutive impulses. Assume an underdamped case so define w₁² = w₀² - β ².

(a) Solve the differential equation describing the motion of the mass for the n=1 case, include damping. Let x(0)=x0 and v(0)=0. You will need to use the laplace argument to solve the equation. Thus, defining the differential equation as eq you can type: dsolve({eq,x(0)=x0,D(x)(0)=0},x(t),method=laplace);

Identify the homogeneous solution, xh, by setting p0=0 and a particular solution by setting x0=0. For the particular solution, xp, define it as a sum of solutions for j = 1 to n. It would be wise to define t0 as j*t and assume it > 0. Define the general solution, X, as a function of n, t and t.

Hints You should restart and use the following:

eq:= diff(x(t),t,t) + 2*beta*diff(x(t),t) + (omega1^2 + beta^2)*x(t)=Fdrive/m;

Fdrive := p0*Dirac(t-t0);

assume(t0>0):

sol :=dsolve({eq,x(0)=x0,D(x)(0)=0},x(t),method=laplace);

xh :=rhs(subs(p0=0,sol));

subs({x0=0,t0=j*tau},sol);

xp := Sum(rhs(%),j=1..n);

(b) Set x0 = 1, p0 = 1, β = 1/10, w0:=1, w1 = sqrt(w0²- β ²), T = 2*π / w1, and m = 1. Plot X from 0 to t = 4*T for the following values of (n, t): (0,0) [this is the undriven HO], (1,1), (4, T), (20,1). Try to explain what you see.

Hints Here you use:

X:=unapply(xh+xp,n,tau,t):

x0 :=1: p0 :=1: beta:= 1/10: omega0:=1: omega1:=sqrt(omega0^2-beta^2): T:=2*Pi/omega1: m:=1:

The plots will have the form plot(X(1,1,t),t=0..4*T);