| General Chemistry | ||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
| Organic Chemistry | ||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
| General Physics | ||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
| General Math | ||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
General Physics :: Projectile Motion :: How to Calculate #1
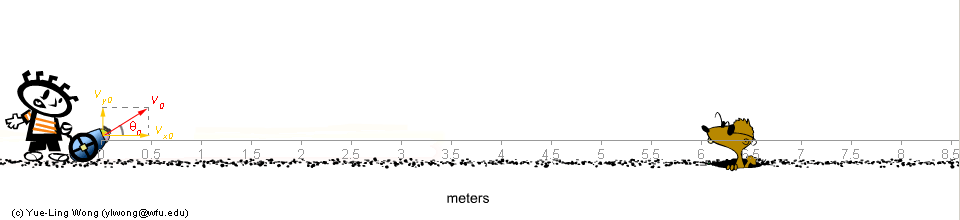
[an error occurred while processing this directive]
| Science Education Tutorials and Practice Exercises | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
General Physics :: Projectile Motion :: How to Calculate #1
[an error occurred while processing this directive] |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||