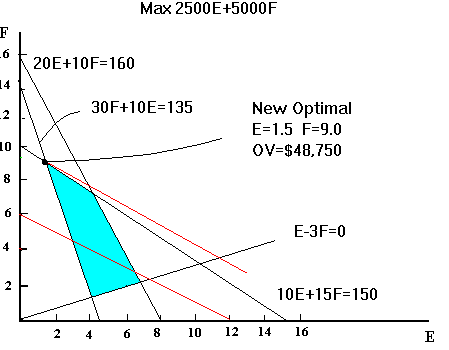
- a) The optimal point is at E=1.5 and F=9.0
- b) The OV is 2500*(1.5)+ 5000*(9.0) = $48,750
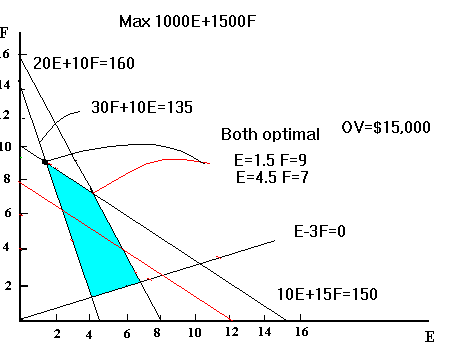
- a) Both (E = 4.5 F= 7) and (E = 1.5 F = 9.0) will be optimal
- b) Objective function value is $15,000 at both points.
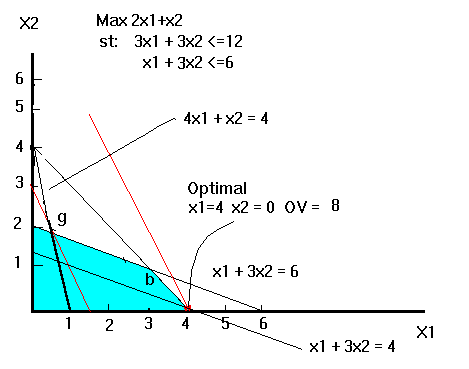
- a)Point x1=4; x2=0 is optimal (OV = 8)
- b) Question is referring to x2. As its profitability
increases, the contour becomes flatter. If it is flat enough the
point b (x1=3; x2=1) becomes optimal. Using the
equality of the OV at these two points we can write:
2*(4) + ?*(0) = 2*(3) +? * (1) Solving for "?" We find that the profitability of x2 has to become at least 2, before the point of optimality shifts to point b where x2 is no longer zero.
We could have reached the same conclusion from the equality of the slopes of 3x1+3x2=12 and the objective contours. The slope of the constraint is -3/3 or -1 the slope of the objective contours is -?/2. Setting these equal and solving for "?" Yields 2 as before. - c) When the Objective function becomes 2x1 + 2x2 both (4,0) and (3,1) are optimal.
- d) Second constraint, x1 + 3x2 <=6, is inactive. Its RHS can increase indefinitely without affecting the optimal point. The RHS can be reduced until it passes through point (4,0). This happens for 1*(4) + 3*(0) = 4. Thus the constraint x1+3x2<=4 passes through point (4,0)and becomes active and any further reductions in its RHS will render point (4,0) infeasible and hence not optimal.
- e) A change in either direction will change the optimal solution.
- f) The constraint in part d is inactive whereas the constraint in e) is active .
- g) Notice that this is an equality constraint therefore the feasible region consists only of the points on the darker line segment in the blue area. Thus the optimal point moves to point g where x1= 6/11 and x2 = 20/11.
- h)The optimal solution is now x1 =1 and x2 = 0.
. Increasing the RHS of a "<=" means that there will be more combinations of decision-variable values that satisfy the constraint. This means that one is relaxing (loosening) the constraint.
Increasing the RHS of a ">=" means that there will be fewer combinations of decision-variable values that satisfy the constraint. This means that one is tightening the constraint.
Tightening a constraint cannot enlarge the feasible set and may leave it unchanged or make it smaller
[go back]
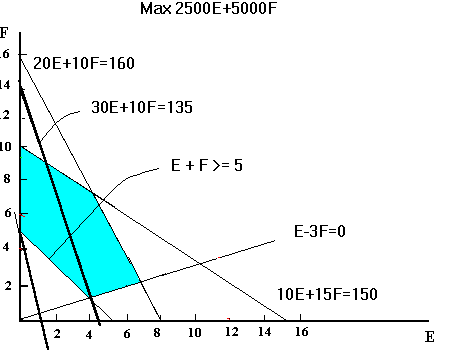
Remembering that there was a redundant constraint E+F>=5 we see from the graph that when the constraint 30E + 10F >= ? passes through the point (0,5) any further reduction in its RHS will not change the feasible region (shown in blue). The constraint passes through that point when its RHS = 30*(0) + 10 *(5) =50.