Student Calculus Library

To use the commands in the student calculus library, give the with(student); command. Don't

forget the semicolon that must end every maple command. A list of the commands in the student

library will be shown.

> with(student);

To draw a picture showing the approximation of the area under a curve using rectangles, the

commands leftbox, rightbox, or middlebox can be used. Three parameters are usually

used with these commands. The first is an expression for the value of the function, the

second is the interval for the area, and the third is the number of subintervals (or rectangles)

that we want to use. First we define e to be the expression for the value of the function.

> e := 1+sqrt(36*x/10);

> plot(e,x=0..10,y=0..10);

> leftbox(e,x=0..10,5);

> leftbox(e,x=0..10,10);

Note that if you don't specify the number of subintervals to use, Maple uses four

subintervals. Four is called the default value for the number of subintervals.

> rightbox(e,x=0..10);

> middlebox(e,x=0..10,6);

The commands leftsum, rightsum, and middlesum can be used to obtain the

numerical approximations.

> leftsum(e,x=0..10,5);

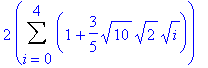
The decimal approximation of an arithmetic expression is obtained by using evalf.

Recall also that % represents the last expression evaluated by Maple.

> evalf(%);

> rightsum(e,x=0..10,10);

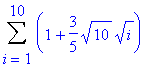
> evalf(%);

> middlesum(e,x=0..10,6);

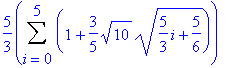
> evalf(%);

>