Go to Optimal value vs. RHS

Optimal \Value vs. Objective Function Coefficients (OFC)

Main results:

  1. When the OFC of a variable increases, if it affects the OV, it will increase it.
  2. The rate of increase in the OV due to increasing OFC is equal to the current value of the variable whose OFC is changing.
  3. If the change in the OFC is helping the OV, and if the change exceeds the allowable limit, the change in the OFC will help the OV at a faster rate.
  4. If the change in the OFC is hurting the OV, and if the change exceeds the allowable limit, the change in the OFC will hurt the OV at a lesser rate.
  5. If a variable is zero at the optimal solution, the reduced cost measures how much more attractive that variable has to get (by changing its OFC) before it can assume a positive value.
  6. Reduced cost of a basic (non-zero) variable is zero.
  7. If the OFC changes sufficiently (>=AD or AI) in a way to make the associated variable more attractive, the value of the variable will increase and vice versa

Let's apply these principles to a number of scenarios: In what follows c denotes the objective function coefficient being varied to study its effect on the solution and the OV; AI denotes allowable increase, AD allowable decrease. o superscript denote the current values of c and OV. The number in parentheses refer to the principle above

Scenarios:
  1. Max: basic variable
  2. Max: non-basic variable
  3. Min: basic variable
  4. Min: non-basic variable
  1. Objective: Max; Variable: non-zero (basic)
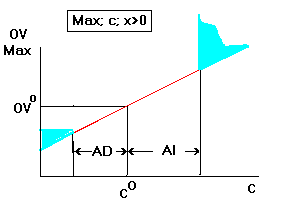
    The OV increases at a rate equal to the value of the variable.(2) When the change exceeds the AI, the solution changes in a way to increase the value of the variable (7). Therefore further changes in the OFC will increase the OV at a higher rate (blue area on the right) (2). Likewise, if the OFC is reduced beyond AD, the value of the variable will be reduced (7) and the OV will decline at a reduced rate (blue area on the left) (2).
    go back

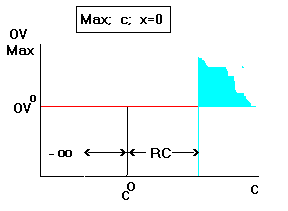  2. Objective: Max; Variable: zero (non-basic)
    Since the value of the variable is zero the OV does not respond to the changes in the OFC (2). If the OFC is reduced, it makes it even more unattractive and hence it will never become positive. However, if the OFC is increased by the amount of the reduced cost (RC), the variable will become positive (5) and further increases in the OFC will increase the OV at this positive rate (blue area on the right)(2).
    go back

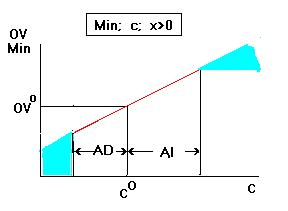  3. Objective: Min; Variable: non-zero (basic)
    As the OFC increases the OV increases at a positive rate equal to the value of the variable (2). When the increase exceeds the AI, the solution changes, the value of the variable is reduced (7). Thus beyond this point the OV increases at a slower rate (blue area on the right) (2). When the OFC decreases so does the OV.(1) When the AD is reached the solution changes in a way to increase the value of the variable (7). Thus beyond this point, the OV will decline even at a faster rate (Blue area on the left)(3).
    go back

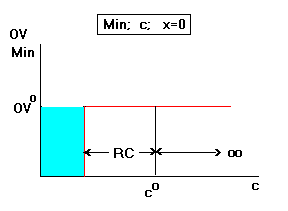  4. Objective: Min; Variable: zero (non-basic)
    The variable is too expensive, so the optimal solution has its value at zero. It can become even more expensive without bound and its value will stay at zero. If, on the other hand, its OFC is reduced and it became less expensive by at least the amount of its reduced cost, it may become positive (5). At this time further reduction in its cost will improve (reduce) the OV (blue area on the left.) (3)
    go back