Go to Optimal Value vs. OFC

Optimal Value vs. RHS

Main principles:

  1. A dual price is associated with each constraint.
  2. The dual price measures the improvement in the objective function (OV) per unit of increase in the RHS.
  3. Improvement in a Max problem means increase in OV, while in a Min problem it means decrease in OV.
  4. Increasing the RHS of a "<=" type loosens the constraint and vice versa.
  5. Increasing the RHS of a ">=" type tightens the constraint and vice versa.
  6. Tightening the constraint can not improve the OV.
  7. Loosening a constraint cannot hurt the OV.
  8. An inactive constraint cannot become active by loosening.
  9. The dual price of an inactive constraint is zero.
  10. Generally, the dual price of an active "<=" constraint is positive, while that of ">=" type is negative.
  11. The dual price of an "=" constraint can be positive or negative.
  12. An inactive "<= (>=)" type constraint can be tightened by the amount of slack (surplus).
  13. Within the allowable range of RHS the solution and the OV may change but the dual price will remain constant.
  14. When the change in the RHS is outside the allowable range the dual price may change in a way "to help less and less" or "to hurt more and more."

Let's apply these principles to a number of scenarios: In what follows b denotes the right hand side of a constraint, AI denotes allowable increase, AD allowable decrease. 0 superscript denote the current values of b and OV. The number in parentheses refer to the principle above

Scennarios:
  1. Max <= active
  2. Max <= inactive
  3. Max >= active
  4. Max >= inactive
  5. Min <= active
  6. Min <= inactive
  7. Min >= active
  8. Max >= inactive
    1. Objective:Max Constraint: active less-than-or-equal-to.
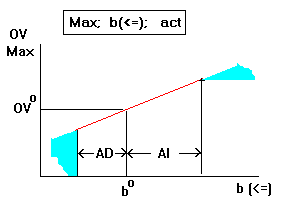      Here the dual price is >0. As the RHS (b) increases, the OV improves (increases) at a rate equal to the dual price (2). The dual price stays constant in the allowable interval (13). When the change in b exceeds the AI the dual price may be reduced (increasing the RHS is helping but after this point the rate of improvement will be dampened). So, the OV will be somewhere in the blue area on the right (14). Likewise if b is curtailed by more than AD the dual price may get larger (reducing the RHS is hurting but after the threshold is reached it will start hurting even more.) The OV therefore will be somewhere in the blue area on the left. (14) This relationship actually illustrates one of the main laws of micro economic theory. Anybody remember what this is? If you do, send me an e-mail . go back

    2. Objective: Max Constraint inactive less-than-or-equal-to.
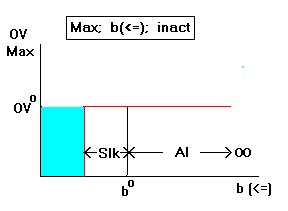      The dual price is zero (9) and the constraint can be loosened indefinitely (8). The OV does not change until the constraint is tightened by the amount of allowable decrease which is equal to slack (Slk) (12). When this point is reached the constraint becomes active and OV may start going down (blue area on the left) (14). go back

    3. Objective: Max; Constraint: active greater-than-or-equal-to.
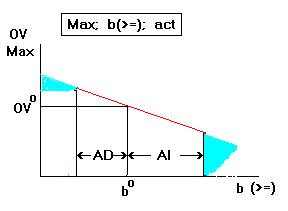      Increasing the RHS tightens the constraint (5) and reduces the OV at the rate of the dual price (2). When upper end of the interval is reached the dual price may decrease (become a larger negative number) and begin to reduce the OV at even a faster rate (blue area on the right) (14). When lower end is reached dual price may become larger and help the OV at a dampened rate (blue area on the left) (14). go back
    4. Objective: Max; Constraint: inactive greater-than-or-equal-to.
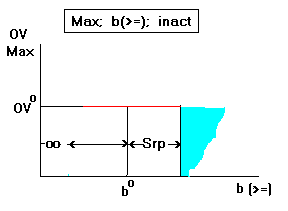      The RHS can be made arbitrarily small (8) and can be tightened by as much as the amount of surplus (Srp) (12). When that happens the constraint will become active and any further tightening will make the dual price negative (10) and hence cause a drop in the OV (blue area on the right) (14). go back
    5. Objective:Min Constraint: active less-than-or-equal-to.
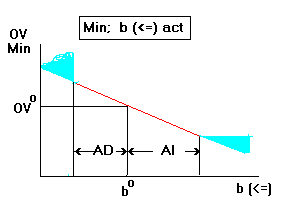      As a "<=" type active constraint is loosened (increase the RHS) the objective improves (7) --goes down in minimization. Since a positive change is associated with positive improvement in the OV the dual price is positive (2). If the increase in the RHS exceeds the allowable increase the rate of improvement will be dampened (blue area on the right) (14). If the RHS is tightened beyond the allowable decrease, the rate of deterioration may be higher (blue area on the left) (14) go back
    6. Objective:Min Constraint: inactive less-than-or-equal-to.
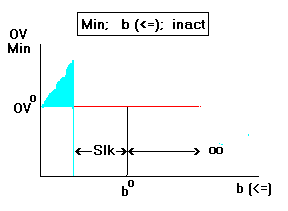      Dual price is zero (9); it will remain zero no matter by how much the constraint is loosened (RHS increased) (8). It can however be tightened by the amount of slack (Slk) (12). When that happens the dual price will become positive (10) and any further reduction in the RHS will be associated with deterioration of the OV (blue area on the right) (14). go back
    7. Objective:Min Constraint: active greater-than-or-equal-to.
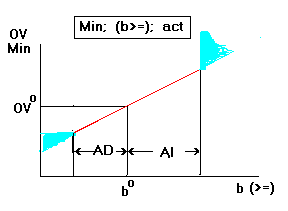      Increasing the RHS tightens the constraint (5) and causes a negative improvement (increase) in the OV (6). If it is tightened beyond AI the rate of increase in the OV will be higher (blue area on the right). If it is loosened by more than AD, the OV will decline (helped) at a slower rate (blue area on the right)(14). go back
    8. Objective:Min Constraint: inactive greater-than-or-equal-to.
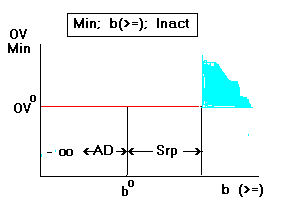      The constraint can be loosened without limit (8), it can be tightened by the amount of the surplus (Srp) (12). If it is tightened beyond that, it will become active, the dual price will become negative (10) and further tightening (increase in RHS) will force an increase (negative improvement) in the OV (6). go back