Measurements

• Use dimensional analysis to determine the units of G:
  F=G(m₁m₂)/r²
  if F is has units of kg m/s², m₁ and m₂ have units of kg, and r has units of m.
  
  Kristen Shumaker (Spring 2014)
  

Motion in One Dimension

• The driver of a car slams on the brakes when he sees that he is about to run into a tree. The car slows down uniformly with an acceleration of 5.60 m/s² for 4.2 s, making skid marks 62.4 m long that ends at the tree. What is the velocity of the car exactly when it hits the tree? (Hint: the answer is not zero)
  
  Killian Wustrow (Spring 2014)
  
• A speedy tortoise can run with a velocity of 0.100 m/s and a hare can run 20.0 times as fast. In a race, they both start at the same time, but the hare stops to rest for 120 seconds. The tortoise wins by a shell (0.200 m). What was the length of the race?
  
  Sam Brashears (Fall 2015)
  
• A hare and a tortoise compete in a race over a straight course 2.40 km long. The tortoise crawls at a speed of 0.180 m/s toward the finish line. The hare runs at a speed of 7.85 m/s toward the finish line for 1.920 km and then stops to tease the slow-moving tortoise as the tortoise eventually passes by. The hare waits for a while after the tortoise passes and then runs toward the finish line again at 7.85 m/s. Both the hare and the tortoise cross the finish line at the exact same instant. Assume both animals, when moving, move steadily at their respective speeds. (a) How far is the tortoise from the finish line when the hare resumes the race? (b) For how long in time was the hare stationary?
  
  Silvia Baila (Fall 2015)
  

Motion in Two Dimensions

• A track star in the broad jump goes into the jump at 12 m/s and launches himself at 20° above the horizontal. How long is he in the air before returning to Earth?
  
  Bryson Rominger (Spring 2014)
  
• A football is thrown upward at a 30.0 angle to the horizontal. To throw a 40.0-m pass, what must be the initial speed of the ball?
  
  Austin French (Fall 2015)
  
• A landscape architect is planning an artificial waterfall in a city park. Water flowing at 1.75 m/s will leave the end of a horizontal channel at the top of a vertical wall h = 3.35 m high, and from there the water falls into a pool (see figure). (a) Will the space behind the waterfall be wide enough for a pedestrian walkway? (Assume that the average pedestrian walkway is 1 m wide.) (b) To sell her plan to the city council, the architect wants to build a model to a scale, which is one-sixteenth actual size. How fast should the water flow in the channel in the model?
  
  
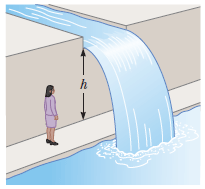
  Max Carter (Fall 2015)
  
• In a local bar, a customer slides an empty beer mug down the counter for a refill. The height of the counter is h. The mug slides off the counter and strikes the floor at distance d from the base of the counter. (a) With what velocity did the mug leave the counter? (Use any variable or symbol stated above along with the following as necessary: g.) (b) What was the direction of the mug's velocity just before it hit the floor? (Use any variable or symbol stated above as necessary.)
  
  Daniel Spieler (Fall 2015)
  
• A ball is thrown horizontally from the top of a building 0.10 km high. The ball strikes the ground at a point 65 m horizontally away from and below the point of release. What is the speed of the ball just before it strikes the ground?
  
  Amanda McAneny (Spring 2014)
  
• Wile E. Coyote has missed the elusive roadrunner once again. This time, he leaves the edge of the cliff at 50.0 m/s horizontal velocity. If the canyon is 100 m deep, how far from the edge of the cliff does the coyote land? How long is he in the air before returning to Earth?
  
  Lauren Lauterbach (Fall 2015)
  
• Garfield kicks Odie at ground level. The Odie is observed to reach his maximum height above ground level 3.0 s after being hit. And 2.5 s after reaching this maximum height, the Odie is observed to barely clear a fence that is 97.5 m from where he was hit. How high is the fence?
  
  Wesley Skidmore (Fall 2015)
  
• A crate of mass m is placed on an incline with θ=30°. a) What is the acceleration of the crate as it slides down the incline? b) Starting from rest, the crate travels a distance d=10.2 m to the bottom of the incline. How long does it take to reach the bottom?
  
  Eric Kandigan (Spring 2014)
  

Laws of Motion

• A 2.65-kg object is moving in a plane, with its x and y coordinates given by x = 6t² − 3 and y = 4t³ + 5, where x and y are in meters and t is in seconds. Find the magnitude of the net force acting on this object at t = 2.20 s.
  
  Zoë Hurtado (Fall 2015)
  
• In the figure shown, the coefficient of kinetic friction between the block and the incline is 0.40. What is the magnitude of the acceleration of the suspended block as it falls? Disregard any pulley mass or friction in the pulley.
  
  
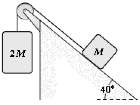
  Caroline Lynott (Spring 2014)
  
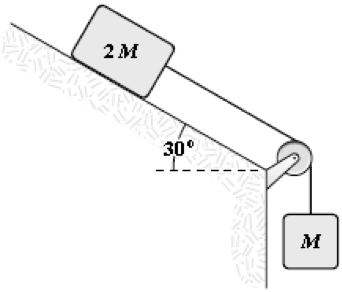
• If F = 40 N and M = 1.5 kg, what is the tension in the string connecting M and 2M? Assume that all surfaces are frictionless.
  
  
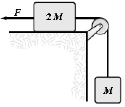
  Manal Ahmidouch (Fall 2015)
  
• If M = 2.0 kg, what is the tension in string 1?
  
  
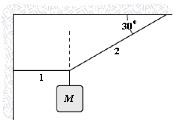
  Lindey Campagne (Spring 2014)
  
• If a = 40° and the tension in string 2 is 30 N, determine M, the mass of the two objects.
  
  
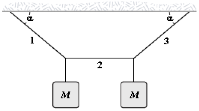
  Fabrice Momo (Spring 2014)
  
• A block is pushed up a frictionless 30° incline by an applied force as shown. If F = 25 N and M = 3.0 kg, what is the magnitude of the resulting acceleration of the block?
  
  
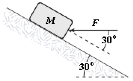
  Emily McCarthy (Fall 2015)
  
• Two blocks of mass m₁ = 3.00 kg and m₂ = 9.00 kg are connected by a massless string that passes over a frictionless pulley (see the figure below). The inclines are frictionless.
  
  
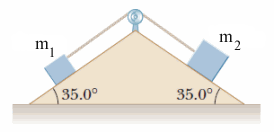
  Brad Feldman (Fall 2015)
  
• The system shown in the figure below has an acceleration of magnitude 0.77 m/s², where m₁ = 4.10 kg and m₂ = 6.60 kg. Assume that the coefficient of kinetic friction between block and incline is the same for both inclines. (a) Find the coefficient of kinetic friction. (b) Find the tension in the string.
  
  
  Laney Vaughan (Fall 2015)
  
• In the figure shown, the coefficient of kinetic friction between the block and the incline is 0.29. What is the magnitude of the acceleration of the suspended block as it falls? Disregard any pulley mass or friction in the pulley.
  
  
  Millie Perez (Fall 2015)
  

Circular Motion

• A race car moving with a constant speed of 60 m/s completes one lap around a circular track in 50 s. What is the magnitude of the acceleration of the race car?
  
  Bailey Goodwin (Spring 2014)
  
• Jeff Gordon is driving a car into a curve. The radius of the curve is 1,000 m and the coefficient of static friction between his tires and the pavement is 0.500. Find the maximum speed he must have to make the turn without skidding?
  
  Hugh Thompson (Fall 2015)
  

Energy of a System

• A block is pushed across a rough horizontal surface from point A to point B by a force (magnitude P = 5.4 N) as shown in the figure. The magnitude of the force of friction acting on the block between A and B is 1.2 N and points A and B are 0.5 m apart. If the kinetic energies of the block at A and B are 4.0 J and 5.6 J, respectively, how much work is done on the block by the force P between A and B?
  
  
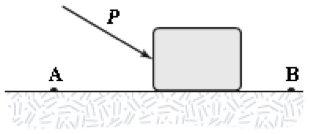
  Carson Wigley (Spring 2014)
  
• Two clowns are launched from the same spring-loaded circus cannon with the spring compressed the same distance each time. Clown A has a 40-kg mass; clown B a 60-kg mass. What is the relation between their speeds at the instant of launch?
  
  Emmy Feng (Fall 2015)
  
• A quarterback throws a football of mass 0.15 kg at a speed of 40 m/s and initial angle of 30°. What is the kinetic energy of the football at the highest point of the trajectory? (Hint: The answer is not 0 J.)
  
  Chirag Patel (Spring 2014)
  
• Hooke's law describes a certain light spring of unstretched length 32.1 cm. When one end is attached to the top of a doorframe and a 7.52 kg object is hung from the other end, the length of the spring is 41.6 cm. (a) Find its spring constant. (b) The load and the spring are taken down. Two people pull in opposite directions on the ends of the spring, each with a force of 182 N. Find the length of the spring in this situation.
  
  Hannah Johnston (Fall 2015)
  
• A 10-kg block on a horizontal frictionless surface is attached to a light spring (force constant = 0.80 kN/m). The block is initially at rest at its equilibrium position when a force (magnitude P = 80 N) acting parallel to the surface is applied to the block, as shown. What is the speed of the block when it is 0.13 m from its equilibrium position?
  
  
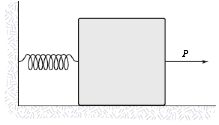
  Addie Rodes Carr (Fall 2015)
  
• The horizontal surface on which the block slides is frictionless. The speed of the block before it touches the spring is 6.0 m/s. How fast is the block moving at the instant the spring has been compressed 15 cm? k = 2.0 kN/m
  
  
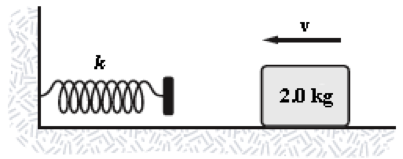
  Crystal Aguero-Norman (Spring 2014)
  
• A skater extends her arms horizontally, holding a 5-kg mass in each hand. She is rotating about a vertical axis with an angular velocity of one revolution per second. If she drops her hands to her sides, what will the final angular velocity (in rev/s) be if her moment of inertia remains approximately constant at 5 kg⋅m², and the distance of the masses from the axis changes from 1 m to 0.1 m?
  
  Kaycie Van Driel (Fall 2015)
  
• A 2.0-kg block situated on a frictionless incline is connected to a light spring (k = 100 N/m), as shown. The block is released from rest when the spring is unstretched. The pulley is frictionless and has negligible mass. What is the speed of the block when it has moved 0.20 m down the plane?
  
  
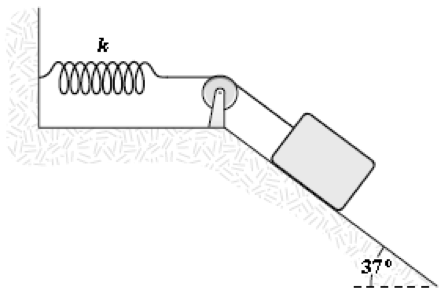
  Brady Gales (Fall 2015)
  

Conservation of Energy

• A 0.04 kg ball is thrown from the top of a 30 m tall building (point A) at an unknown angle above the horizontal. As shown in the figure, the ball attains a maximum height of 10 m above the top of the building before striking the ground at point B. If air resistance is negligible, what is the value of the kinetic energy of the ball at B minus the kinetic energy of the ball at A (K_B − K_A)?
  
  
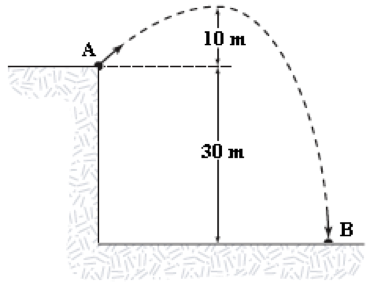
  Erin Christensen (Spring 2014)
  
• A 0.80 kg object tied to the end of a 2.0 m string swings as a pendulum. At the lowest point of its swing, the object has a kinetic energy of 10 J. Determine the speed of the object at the instant when the string makes an angle of 50° with the vertical.
  
  Carly Brailer (Spring 2014)
  
• A 2.0-kg mass swings at the end of a light string (length = 3.0 m). Its speed at the lowest point on its circular path is 6.0 m/s. What is its kinetic energy at an instant when the string makes an angle of 50° with the vertical?
  
  Nicole Rojas (Fall 2015)
  
• A 2.0 kg block slides down a frictionless incline from point A to point B. A force (magnitude P = 3.0 N) acts on the block between A and B, as shown. Points A and B are 2.0 m apart. If the kinetic energy of the block at A is 10 J, what is the kinetic energy of the block at B?
  
  
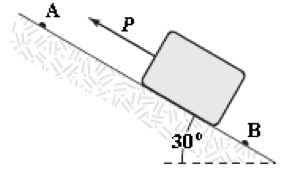
  Zac Riley (Spring 2014)
  
• The two masses in the figure are released from rest. After the 3.0 kg mass has fallen 1.5 m, it is moving with a speed of 3.8 m/s. What is the change in mechanical energy done on the system during this time interval by the frictional force on the 2.0 kg mass?
  
  
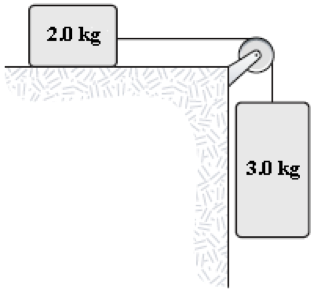
  Lauren Robertson (Fall 2015)
  
• A 1.2-kg mass is projected up a rough circular track (radius = 0.80 m) as shown. The speed of the mass at point A is 8.4 m/s, and at point B, it is 5.6 m/s. What is the change in mechanical energy between A and B caused by the force of friction?
  
  
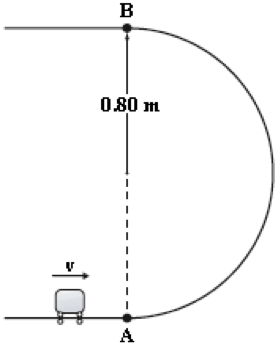
  Erik Butcher (Spring 2014)
  



• Two clowns are separately launched from the same spring-loaded circus cannon with the spring compressed the same distance each time. Clown A has a 40-kg mass; clown B a 60-kg mass. The relation between their speeds at the instant of launch is:
  
  Mary Byrd Ewell (Spring 2014)
  



• A large spring is used to stop the cars after they come down the last hill of a roller coaster. The cars start at rest at the top of the hill and are caught by a mechanism at the instant their velocities at the bottom are zero. Compare the compression of the spring, x_A, for a fully loaded car with that, x_B, for a lightly loaded car when m_A = 2m_B.
  
  
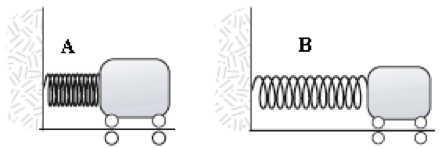
  Dani Monroe (Spring 2014)
  
  



• A 2.0 kg block slides down a plane (inclined at 40° with the horizontal) at a constant speed of 5.0 m/s. At what rate is the gravitational force on the block doing work?
  
  Diamond Cherry (Spring 2014)
  

Linear Momentum and Collisions

• A 3.0-kg object moving 8.0 m/s in the positive x direction has a one-dimensional elastic collision with an object (mass = M) initially at rest. After the collision the object of unknown mass has a velocity of 6.0 m/s in the positive x direction. What is M?
  
  Amanda Murphy (Fall 2015)
  
• Supergirl claims she can run with as much momentum as a 3.00-g bullet moving with a speed of 1,500 m/s. Supergirl has a mass of 50 kg. What must be Supergirl’s speed if her claim is valid?
  
  Nia McIntosh (Fall 2015)
  
• A 10-g bullet moving 1 000 m/s strikes and passes through a 2.0-kg block initially at rest, as shown. The bullet emerges from the block with a speed of 400 m/s. To what maximum height will the block rise above its initial position?
  
  
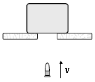
  Anita Patel (Fall 2015)
  
• A 12-g bullet moving horizontally strikes and remains in a 3.0-kg block initially at rest on the edge of a table. The block, which is initially 80 cm above the floor, strikes the floor a horizontal distance of 120 cm from its initial position. What was the initial speed of the bullet?
  
  Adeline Ding (Fall 2015)
  

Rotation of a Rigid Object About a Fixed Axis

• A discus thrower accelerates a discus from rest to a speed of 25.7 m/s by whirling it through 1.28 rev. Assume the discus moves on the arc of a circle 1.04 m in radius. (a) Calculate the final angular speed of the discus. (b) Determine the magnitude of the angular acceleration of the discus, assuming it to be constant. (c) Calculate the time interval required for the discus to accelerate from rest to 25.7 m/s.
  
  Emily Machiele (Fall 2015)
  
• A satellite is in a circular orbit 600 km above the Earth's surface. The acceleration of gravity is 8.21 m/s² at this altitude. The radius of the Earth is 6 400 km. Determine a) the speed of the satellite, and b) the time to complete one orbit around the Earth. (Hint: For (a), note the direction of the acceleration of gravity.)
  
  Lauren Clopper (Fall 2015)
  
• Find the net torque on the wheel in the figure below about the axle through O, taking a = 13.0 cm and b = 25.0 cm. (Assume that the positive direction is counterclockwise.)
  
  
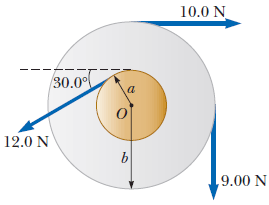
  Brittany Kirby (Fall 2015)
  

Angular Momentum

• A puck on a frictionless air hockey table has a mass of 5.0 kg and is attached to a cord passing through a hole in the surface as in the figure. The puck is revolving at a distance 2.0 m from the hole with an angular velocity of 3.0 rad/s. The angular momentum of the puck (in kg⋅m²/s) is:
  
  
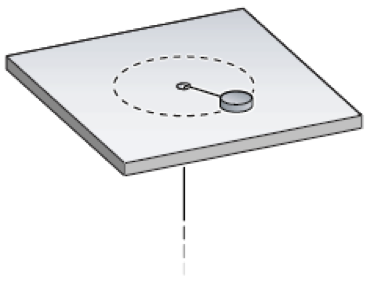
  Katie Balardi (Spring 2014)
  
• A student sits on a freely rotating stool holding two dumbbells, each of mass 2.99 kg (see figure below). When his arms are extended horizontally (Figure a), the dumbbells are 1.05 m from the axis of rotation and the student rotates with an angular speed of 0.752 rad/s. The moment of inertia of the student plus stool is 2.59 kg · m2 and is assumed to be constant. The student pulls the dumbbells inward horizontally to a position 0.302 m from the rotation axis (Figure b). (a) Find the new angular speed of the student. (b) Find the kinetic energy of the rotating system before and after he pulls the dumbbells inward.
  
  
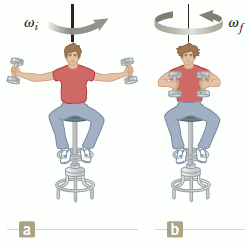
  Grace Babcock (Fall 2015)
  
• A puck of mass m₁ = 70.0 g and radius r₁ = 4.40 cm glides across an air table at a speed of v with arrow = 1.50 m/s as shown in Figure a. It makes a glancing collision with a second puck of radius r₂ = 6.00 cm and mass m₂ = 100 g (initially at rest) such that their rims just touch. Because their rims are coated with instant-acting glue, the pucks stick together and rotate after the collision (Figure b). (a) What is the magnitude of the angular momentum of the system relative to the center of mass? (b) What is the angular speed about the center of mass?
  
  
  YoonSun Jee (Fall 2015)
  
• A space station is constructed in the shape of a hollow ring of mass 5.80 x 10⁴ kg. Members of the crew walk on a deck formed by the inner surface of the outer cylindrical wall of the ring, with radius 145 m. At rest when constructed, the ring is set rotating about its axis so that the people inside experience an effective free-fall acceleration equal to g. (See figure below.) The rotation is achieved by firing two small rockets attached tangentially to opposite points on the rim of the ring. (a) What angular momentum does the space station acquire? (b) For what time interval must the rockets be fired if each exerts a thrust of 130 N?
  
  
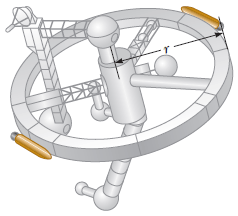
  Ike Osuorah (Fall 2015)
  

Universal Gravitation

• The period of a satellite circling planet Romulus is observed to be 84 s when it is in a circular orbit with a radius of 8.0 x 10⁶ m. What is the mass of planet Romulus?
  
  Allison Leon (Spring 2014)
  
• What is the kinetic energy of a 200 kg satellite as it follows a circular orbit of radius 8.0 x 10⁶ m around the Earth? (Mass of Earth = 6.0 x 10²⁴ kg.)
  
  Victoria DeLuca (Spring 2014)
  

Static Equilibrium

• A horizontal uniform meter stick supported at the 50-cm mark has a mass of 0.50 kg hanging from it at the 20 cm mark and a 0.30 kg mass hanging from it at the 60 cm mark. Determine the position on the meter stick at which one would hang a third mass of 0.60 kg to keep the meter stick balanced.
  
  Samantha Zaveda (Spring 2014)
  
• A uniform plank of length 2.00 m and mass 26.0 kg is supported by three ropes as indicated by the blue vectors in the figure below. Find the tension in each rope when a 705 N person is d = 0.350 m from the left end.
  
  
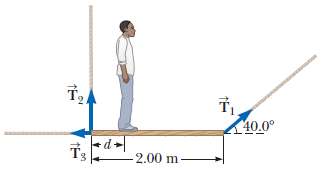
  Megan Blackstock (Fall 2015)
  
• Sir Lost-a-Lot dons his armor and sets out from the castle on his trusty steed (see figure below). Usually, the drawbridge is lowed to a horizontal position so that the end of the bridge rests on the stone ledge. Unfortunately Lost-a-Lot's squire didn't lower the drawbridge far enough and stopped it at θ = 20.0° above the horizontal. The knight and his horse stop when their combined center of mass is d = 1.00 m from the end of the bridge. The uniform bridge is ℓ = 7.00 m long and has a mass of 2 100 kg. The lift cable is attached to the bridge 5.00 m from the hinge at the castle end and to a point on the castle wall h = 12.0 m above the bridge. Lost-a-Lot's mass combined with his armor and steed is 950 kg. (a) Determine the tension in the cable. (b) Determine the horizontal force component acting on the bridge at the hinge. (c) Determine the vertical force component acting on the bridge at the hinge.
  
  
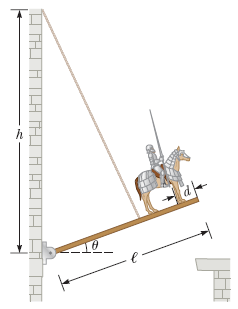
  Lauren Bosway (Fall 2015)
  

Elasticity

• A 20 m long steel wire (cross-section 1.0 cm², Young's modulus 2.0 × 10¹¹ N/m²), is subjected to a load of 25,000 N. How much will the wire stretch under the load?
  
  Collin Preston (Spring 2014)
  
• A stonecutter's chisel has an edge area of 0.7 cm². If the chisel is struck with a force of 42 N, what is the pressure exerted on the stone?
  
  Kurt Walker (Spring 2014)
  
• For safety in climbing, a mountaineer uses a 50 m long nylon rope that is 1.0 cm in diameter. When supporting a 90 kg climber, the rope elongates 1.6 m. Find the Young's modulus for the rope material.
  
  Alex Eller (Spring 2014)
  

Fluid Mechanics

• A hydraulic lift raises a 2,000 kg automobile when a 500 N force is applied to the smaller piston. If the smaller piston has an area of 10 cm², what is the cross-sectional area of the larger piston?
  
  Madie Greer (Spring 2014)
  

Oscillatory Motion

• In an engine, a piston oscillates with simple harmonic motion so that its position varies according to x = 4.00 cos (t + π/8) where x is in centimeters and t is in seconds. What is the acceleration of the piston at t=0.0 s?
  
  Connor Naden (Fall 2015)