| MWF 10 AM-10:50 PM | OPL 103 | http://www.wfu.edu/~natalie/f13phy711/ |
| Instructor: Natalie Holzwarth | Phone:758-5510 | Office:300 OPL | e-mail:natalie@wfu.edu |
| Date | F&W Reading | Topic | Assignment | |
| 1 | Wed, 8/28/2013 | Chap. 1 | Review of basic principles;Scattering theory | #1 |
| 2 | Fri, 8/30/2013 | Chap. 1 | Scattering theory continued | #2 |
| 3 | Mon, 9/02/2013 | Chap. 1 | Scattering theory continued | #3 |
| 4 | Wed, 9/04/2013 | Chap. 2 | Accelerated Coordinate Systems | #4 |
| 5 | Fri, 9/06/2013 | Chap. 3 | Calculus of variations | #5 |
| 6 | Mon, 9/09/2013 | Chap. 3 | Calculus of variations -- continued | |
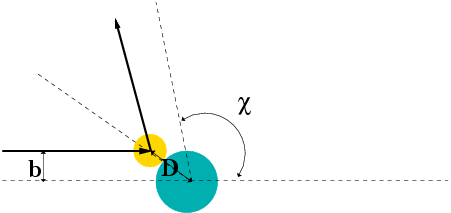
| 7 | Wed, 9/11/2013 | Chap. 3 | Calculus of variations applied to Lagrangians | #6 |
| 8 | Fri, 9/13/2013 | Chap. 3 | Lagrangian mechanics | #7 |
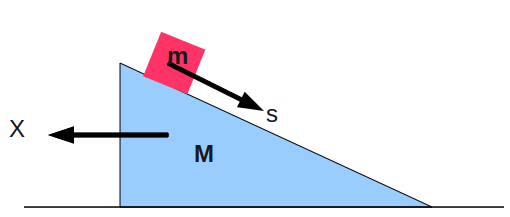
| 9 | Mon, 9/16/2013 | Chap. 3 & 6 | Lagrangian mechanics | #8 |
| 10 | Wed, 9/18/2013 | Chap. 3 & 6 | Lagrangian mechanics | #9 |
| 11 | Fri, 9/20/2013 | Chap. 3 & 6 | Lagrangian & Hamiltonian mechanics | #10 |
| 12 | Mon, 9/23/2013 | Chap. 3 & 6 | Hamiltonian formalism | #11 |
| 13 | Wed, 9/25/2013 | Chap. 3 & 6 | Hamiltonian formalism | #12 |
| 14 | Fri, 9/27/2013 | Chap. 3 & 6 | Hamiltonian formalism | #13 |
| 15 | Mon, 9/30/2013 | Chap. 4 | Small Oscillations | #14 |
| 16 | Wed, 10/02/2013 | Chap. 4 | Small Oscillations | |
| 17 | Fri, 10/04/2013 | Chap. 4 | Small Oscillations | #15 |
| 18 | Mon, 10/07/2013 | Chap. 4 & 7 | Small Oscillations and waves | #16 |
| 19 | Wed, 10/09/2013 | Chap. 7 | Wave equation | |
| Fri, 10/11/2013 | No class (Fall Break) | |||
| 20 | Mon, 10/14/2013 | Chap. 7 | Wave equation (Presentation topic due) | #17 | 21 | Wed, 10/16/2013 | Chap. 7 | Mathematical methods | #18 |
| 22 | Fri, 10/18/2013 | Chap. 7 | Mathematical methods | #19 |
| 23 | Mon, 10/21/2013 | Chap. 5 | Rigid rotations | #20 |
| 24 | Wed, 10/23/2013 | Chap. 5 | Rigid rotations | #21 |
| 25 | Fri, 10/25/2013 | Chap. 5 | Rigid rotations | |
| Mon, 10/28/2013 | No class | Take-home exam | ||
| Wed, 10/30/2013 | No class | Take-home exam | ||
| Fri, 11/01/2013 | No class | Take-home exam | ||
| 26 | Mon, 11/04/2013 | Chap. 8 | Oscillations in two-dimensional membranes | Take-home exam due |
| 27 | Wed, 11/06/2013 | Chap. 9 | Physics of fluids | #22 |
| 28 | Fri, 11/08/2013 | Chap. 9 | Physics of fluids | #23 |
| 29 | Mon, 11/11/2013 | Chap. 9 | Sound Waves | #24 |
| 30 | Wed, 11/13/2013 | Chap. 9 | Sound Waves | #25 |
| 31 | Fri, 11/15/2013 | Chap. 9 | Non linear effects in Sound | #26 |
| 32 | Mon, 11/18/2013 | Chap. 10 | Surface waves | |
| 33 | Wed, 11/20/2013 | Chap. 10 | Surface waves | |
| 34 | Fri, 11/22/2013 | Chap. 11 | Heat conduction | |
| 35 | Mon, 11/25/2013 | Chap. 12 | Viscous fluids | |
| Wed, 11/27/2013 | Thanksgiving Holiday | |||
| Fri, 11/29/2013 | Thanksgiving Holiday | |||
| 36 | Mon, 12/02/2013 | Student presentations I | ||
| 37 | Wed, 12/04/2013 | Student presentations II | ||
| 38 | Fri, 12/06/2013 | Student presentations III | ||
| Mon, 12/09/2013 | Begin Take-home final |
|
|

|
Finish reading Chapter 1 in Fetter & Walecka.
Read Chapter 2 in Fetter & Walecka.
Start reading Chapter 3 in Fetter & Walecka.
Continue reading Chapter 3 in Fetter & Walecka.
|
|
Continue reading Chapters 3 and 6 in Fetter & Walecka.
Continue reading Chapters 3 and 6 in Fetter & Walecka.
Continue reading Chapters 3 and 6 in Fetter & Walecka.
Continue reading Chapter 6 in Fetter & Walecka.
Finish reading Chapter 6 in Fetter & Walecka.
Finish reading Chapter 6 in Fetter & Walecka.
Read parts of the paper by Hans C. Andersen "Molecular dynamics simulations at constant pressure and/or temperature" in which he constructs a Lagrangian function to represent a system of particles held at constant pressure α.
Continue reading Chapter 4 in Fetter & Walecka.
Finish reading Chapter 4 and start Chapter 7 in Fetter & Walecka.
Continue reading Chapter 7 in Fetter & Walecka and the lecture notes.
|
Finish reading Chapter 7 in Fetter & Walecka
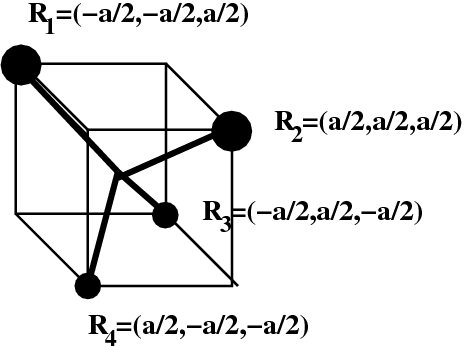 The above figure shows an object with four particles held
together with massless bonds at the coordinates shown. The
masses of the particles are m1=m2 ≡ 2m and m3=m4 ≡ m.
The above figure shows an object with four particles held
together with massless bonds at the coordinates shown. The
masses of the particles are m1=m2 ≡ 2m and m3=m4 ≡ m.
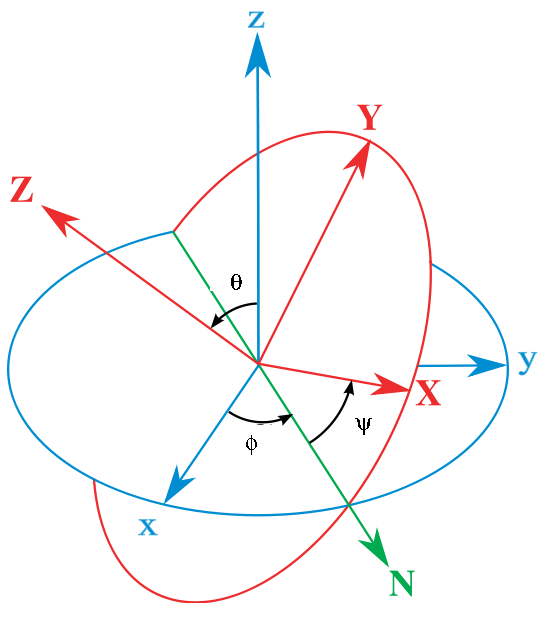 In this case, the first rotation is about the original ∧z axis by ϕ
corresponding to the rotation matrix
In this case, the first rotation is about the original ∧z axis by ϕ
corresponding to the rotation matrix
| (1) |
| (2) |
| (3) |
Continue reading Chapter 9 in Fetter & Walecka.
Continue reading Chapter 9 in Fetter & Walecka.
Continue reading Chapter 9 in Fetter & Walecka.
Continue reading Chapter 9 in Fetter & Walecka.
Finish reading Chapter 9 in Fetter & Walecka.