Brachistochrone Problems in Inverse Square Gravitational Fields

In 1696 Johann Bernoulli posed the following problem: given
two points \(A,B\) find a curve connecting \(A\) and \(B\) such that a particle travelling from \(A\) to \(B\) under the influence of a uniform gravitational
field takes the minimum time. This is called the brachistochrone problem, from the Greek terms brachistos for shortest and chronos for time. It was solved the following year by Leibniz, L'Hospital,
Newton, and others. While the solution to the brachistochrone problem has limited applications, the techniques from calculus used to solve it were novel at the
time. Namely, rudimentary techniques from what would later be called the calculus
of variations were developed. Euler and Lagrange later formalized these initial approaches into their celebrated necessary conditions for optimality, what we now call
the Euler-Lagrange equations. For certain types of functionals, this approach reduces
the optimization problem to solving a diferential equation, i.e. the Euler-Lagrange
equation corresponding to the functional. Indeed, the reduction of an optimization
problem to that of solving a di
erential equation can be directly applied to many
classical optimization problems such as the isoperimetric problem, determining
the shape of a minimal surface and calculating the path of a geodesic on a
surface. Moreover, in classical mechanics the dynamics of a system can be derived
using the Euler-Lagrange equations to extremize the so called "action" of the system. This approach to classical mechanics is equivalent to Newtonian mechanics but
leads to deeper insights which are critical to our current mathematical understanding
of quantum mechanics, general relativity, and other branches of physics.
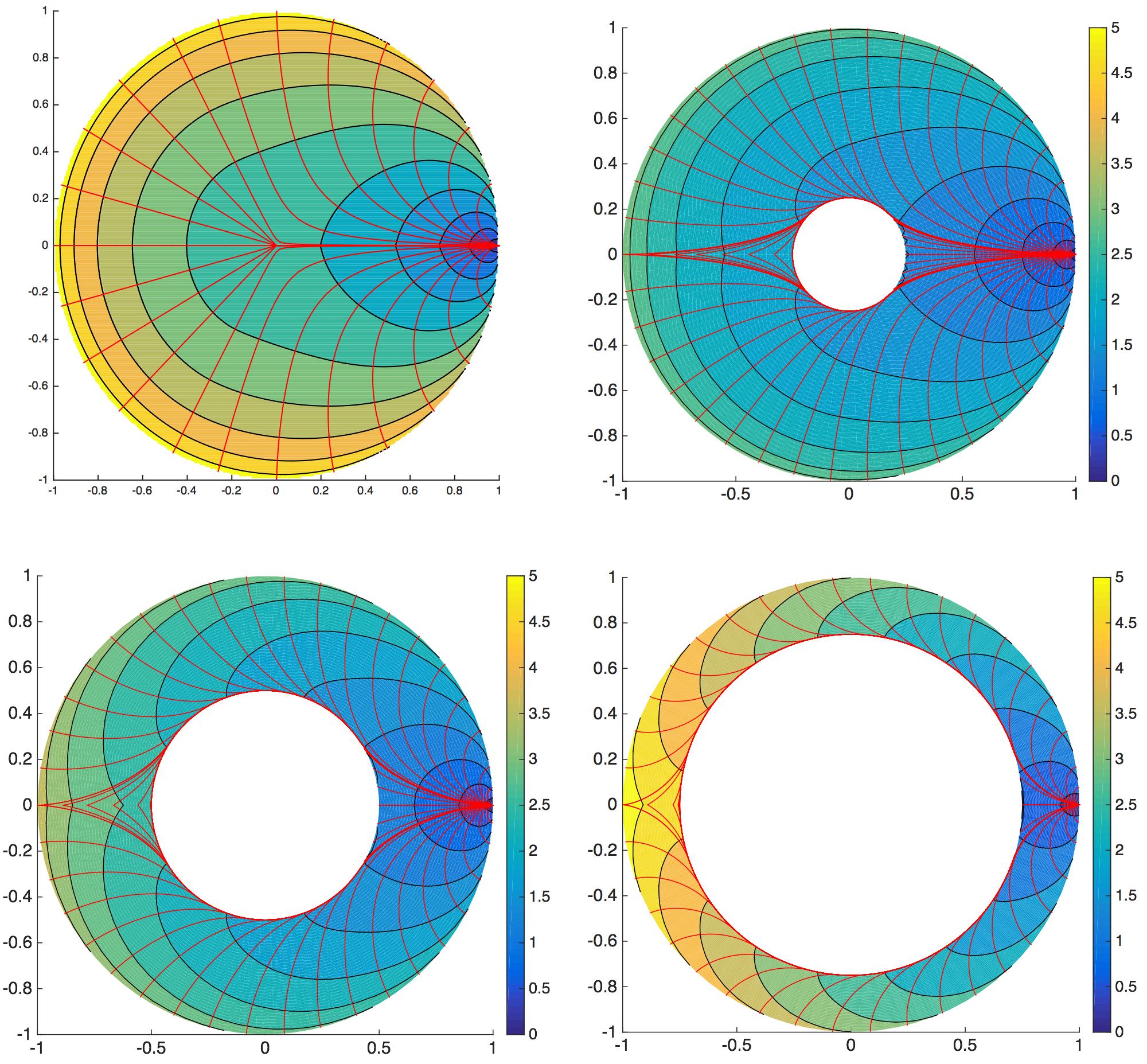
As an undergraduate research project at Brown University, Christopher (Chris) Grimm colaborated with me on a project to understand brachistochrone problems in inverse square gravitational fields. Specifically, Chris's work focused on studying the existence and regularity of minimizers to the following variational problem: \[\min_{\alpha \in \mathcal{A}} T[\alpha] = \min_{\alpha\in \mathcal{A}}\int_{0}^{1}\frac{\|\alpha^{\prime}(s)\|}{\sqrt{\|\alpha(s)\|^{-1}- 1}} ds\] where the admissible set \(\mathcal{A}\) consists of absolutely continuous curves that connect \(A\) and \(B\). While the Euler-Lagrange equations can be directly solved for this problem, they do not provide the complete picture. In particular, as necessary conditions for optimality their derivation implicitly assumes existence and smoothness of a minimum. For Chris's problem these assumptions were naive. In particular, using the weak formulation of the Euler-Lagrange equations Chris rigorously proved that minimizers to this problem are necessarly piecewise smooth curves. The techniques used by Chris consisted of "patching together" local solutions of the Euler-Lagrange equations at the singular origin. These solution curves as well as Chris's construction are illustrated in the figure below. Chris also showed that for annular domains that excise the singular origin, his weak solutions curves are obtained in the limit of vanishing inner radius. This work has been published in [1] and is an interesting example of a variational problem in which it is necessary to apply more sophisticated tools from analysis to study an applied problem.
References:
As an undergraduate research project at Brown University, Christopher (Chris) Grimm colaborated with me on a project to understand brachistochrone problems in inverse square gravitational fields. Specifically, Chris's work focused on studying the existence and regularity of minimizers to the following variational problem: \[\min_{\alpha \in \mathcal{A}} T[\alpha] = \min_{\alpha\in \mathcal{A}}\int_{0}^{1}\frac{\|\alpha^{\prime}(s)\|}{\sqrt{\|\alpha(s)\|^{-1}- 1}} ds\] where the admissible set \(\mathcal{A}\) consists of absolutely continuous curves that connect \(A\) and \(B\). While the Euler-Lagrange equations can be directly solved for this problem, they do not provide the complete picture. In particular, as necessary conditions for optimality their derivation implicitly assumes existence and smoothness of a minimum. For Chris's problem these assumptions were naive. In particular, using the weak formulation of the Euler-Lagrange equations Chris rigorously proved that minimizers to this problem are necessarly piecewise smooth curves. The techniques used by Chris consisted of "patching together" local solutions of the Euler-Lagrange equations at the singular origin. These solution curves as well as Chris's construction are illustrated in the figure below. Chris also showed that for annular domains that excise the singular origin, his weak solutions curves are obtained in the limit of vanishing inner radius. This work has been published in [1] and is an interesting example of a variational problem in which it is necessary to apply more sophisticated tools from analysis to study an applied problem.

References:
- Grimm, C., & Gemmer, J. A. (2017). Weak and strong solutions to the inverse-square brachistochrone problem on circular and annular domains. Involve, a Journal of Mathematics, 10(5), 833-856.
