John A. Gemmer

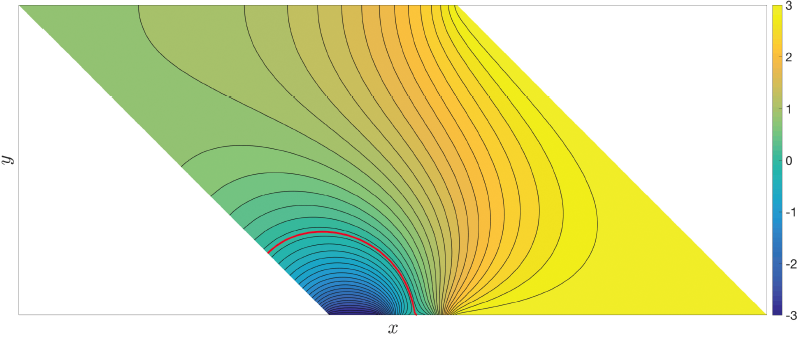In collaboration with Sarah Raynor and Hussein Awala we are studying the regularity properties of solutions to a two dimensional two-phase elliptic free boundary problem on polygonal domains. A prototypical example of such a problem is the determination of steady state velocity fields for the laminar flow of two immiscible, incompressible fluids. It is a classical result that for each fluid there exists a corresponding velocity potential that satisfies Laplace's equation. However, to satisfy local stress balance, a gradient jump condition in the potential must be satisfied at the fluid-fluid interface. In words the problem is the following: find a function which is harmonic where it is nonzero and satisfies a possibly spatially inhomogeneous gradient jump condition across the boundary of its zero set, i.e. the free boundary. We are specifically interested in how the free boundary interacts with Neumann corner points on the boundary. For a smooth harmonic function satisfying Neumann boundary conditions it is clear that the level sets of the function, and in particular the free boundary, will intersect orthogonally with the Neumann boundary. However, depending on the opening angle of the corner, this local condition of orthogonality may contradict continuity of the free boundary away from the corner point. This problem arises in a number of applied areas including, but not limited to, fluid dynamics, electromagnetics and optimal shape design.

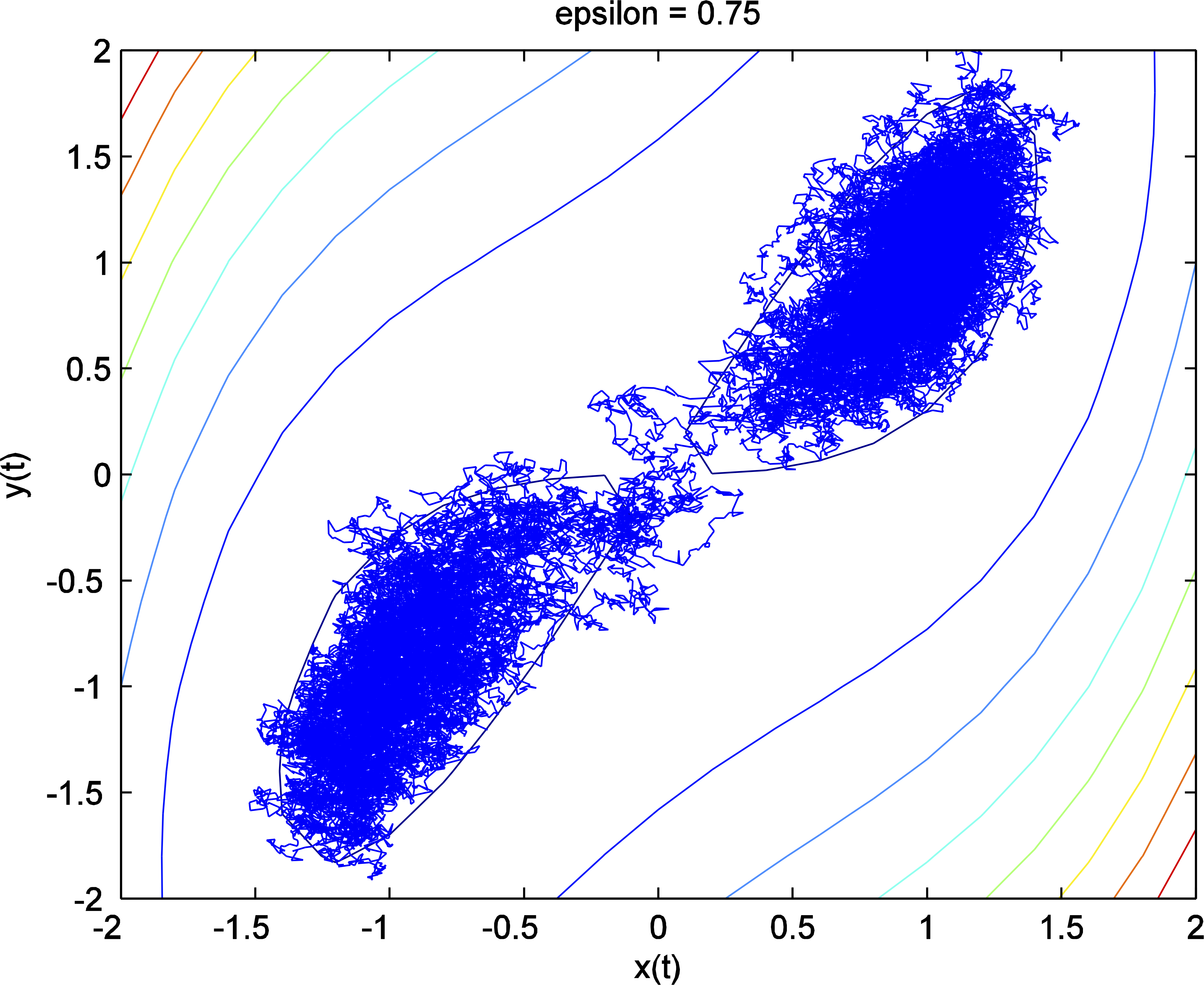Metastability in spatially extended systems is a new area of research for me that has grown out of my interest in energy driven pattern formation. Specifically, my past research in pattern formation focused on understanding the existence and regularity of local minimizers in the so called non-Euclidean model of elasticity. In my prior work I have shown that in certain parameter regimes the global minimizers do not correspond to what is observed experimentally. However, there exist an infinite famly of local minimizers that qualitively resemble what is observed experimentally and within this family the energy barriers between local minimizers is very low. Consequently, these sheets are floppy in the sense that they are easily deformed by weak stresses. Therefore, the buckling pattern of the sheet is sensitive to the dynamics of the swelling process and random fluctuations. The focus of this research is to understand the role that dynamics and noise plays in the selection of local minimum.

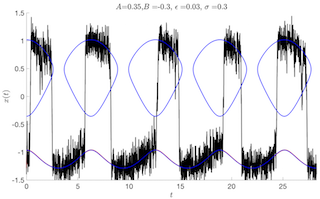In collaboration with Mary Silber, Yuxin Chen, Alexandria Volkening, and Jessica Zanetell I am studying noise induced tipping in periodically forced dynamical systems. It is motivated by the question of whether there is a dominant phase of the periodic forcing where a system is most likely to tip from one attractor to the other, and, if a preferred phase can be identified, what sets it? As a first step in addressing this question we investigate a class of scalar non-autonomous differential equations with weak additive noise. The system possesses a pair of stable periodic solutions, and a tipping event occurs when noise leads to a transition between the two stable states. This simple setting allows us to identify the features of the deterministic system that set the "preferred tipping phase", when it exists. It also illustrates the role of various timescales in the problem in being able to distinguish this phase. It also illustrates the role of various timescales in the problem in being able to distinguish this phase. For example, if the transition from one attractor to the other takes too many cycles of the periodic forcing then it is harder to pin-point the critical phase for tipping, i.e. the periodic forcing is "too fast". The other extreme, of slow forcing, has been extensively studied using asymptotic methods and singular perturbation theory, and is the setting for stochastic resonance. We put particular focus in the intermediate regime between these two extremes.

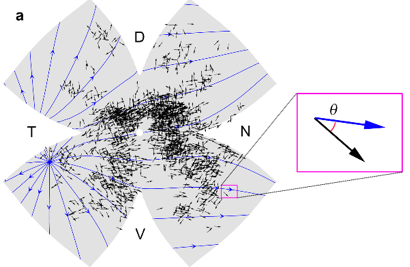In collaboration with Shai Sabbah and David Berson at Brown University I developed a mathematical model for determining the equilibrium shape of a flattened elastic hemisphere from in vitro experiments on dissected retinas. This work has applications to understanding the role direction selective ganglion cells play in image stabilization. By coupling the mathematical model with experimental data we have shown that the preferred directions of the cells vary spatially throughout the retina and in particular the preferred directions are strongly correlated with the gravitational and body axes in the animal.

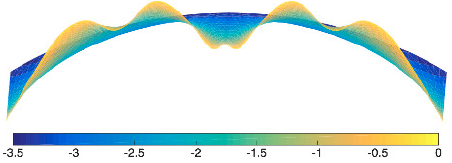The rippling patterns observed in swelling hydrogels, leaves, and torn plastic provide striking examples of periodic and self-similar patterns. While numerical experiments set within the framework of finite elasticity have been able to qualitatively replicate these patterns, they do not provide a complete mathematical understanding of the mechanism behind the self-similar patterns. In my work I seek to understand how such complex geometries are selected by minimization of elastic energy.

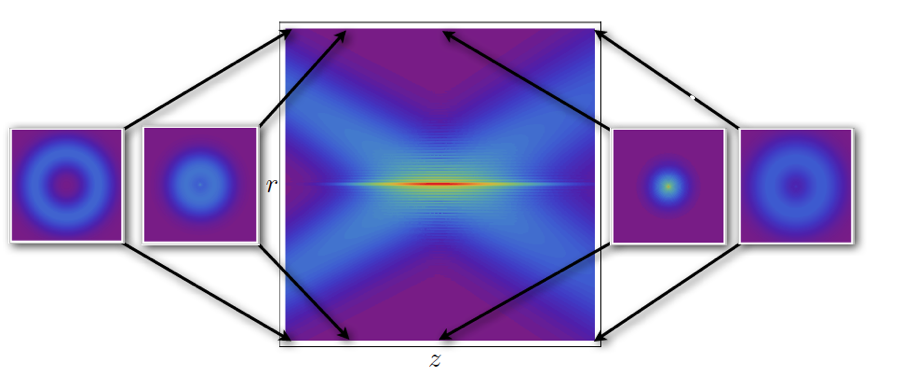In many applications it is desirable to shape a beam or pulse of light so that it has specific properties along the optical axis. In particular, for applications in microscopic imaging, optical tweezers, laser micro-machining, dressing of optical filaments, filament formation and long-range laser ablation, to name a few, it is important to have a well controlled beam with a nearly uniform intensity along the optical axis. However, due to its wave nature localized packets of light will broaden spatially through diffraction. In this work I have studied the problem of phase shaping beams of light into desired intensity profiles.

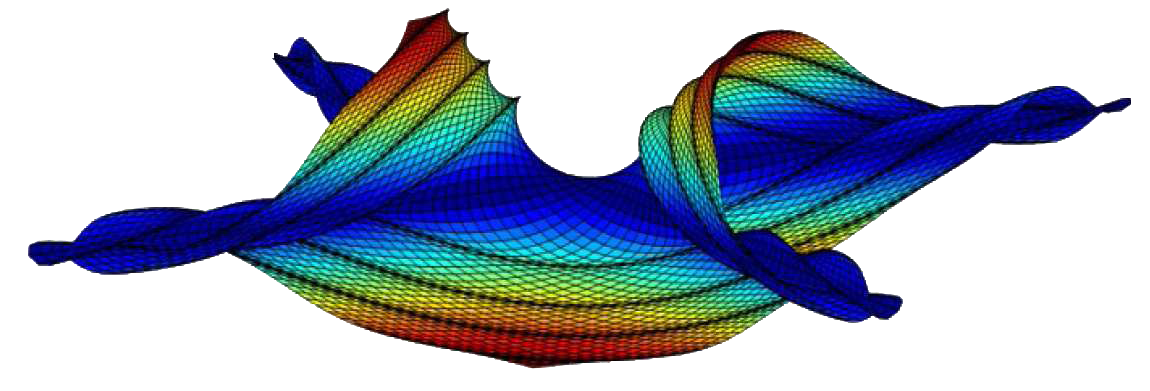In the non-Euclidean formalism of elasticity, swelling in thin elastic sheets is modeled by a Riemannian metric encoding the change in intrinsic distance during the swelling process. The equilibrium configuration is then taken to be a sufficiently smooth deformation that minimizes a non-Euclidean Foppl - von Karman energy that consists of the sum of a strong non-convex stretching energy and a weak convex bending energy that scales with the square of the thickness of the sheet. By studying isometric immersions of the hyperbolic plane, this work seeks to understand the geometry of realized growth patterns in the vanishing thickness limit.