Noise Induced Tipping in Filippov Systems

For her thesis research Jessica (Jessi) Zanetell studied noise induced tipping events between two stable limit cycles for a one dimensional Filippov system with piecewise linear drift and periodic forcing. In this context, by tipping events we mean realizations of the noise that transition from the domain of attraction of one stable limit cycle to another. The specific SDE Jessi considered was the following:
\[\begin{align}
dx&=\begin{cases}
-r_{+}(x-1)+A_{+} \cos(2 \pi t) & \text{if } x> 0\ \\
-r_{-}(x-x_0)+A_{-} \cos(2 \pi (t-p)) & \text{if } x<0\ \\
\end{cases}+\sigma dW,\\
&=f(x,t)+\sigma dW,
\end{align}\]
where \(W\) is a standard Brownian process of strength \(\sigma>0\). This system is a "toy model" of the dynamics of Arctic sea ice thickness with the discontinuity in the drift resulting from a change in the albedo (reflectivity) of ice depending on whether the ocean is in a frozen (\(x<0\)) or unfrozen (\(x>0\)) state. In this toy model the relaxation rates \(r_{\pm}>0\), amplitudes of forcing \(A_{\pm}>0\), and phase shift \(p>0\) can be tuned to control the existence and stability of limit cycles and sliding regions as well as the geometry of the flow. In particular Jessi focused on parameter regimes in which the deterministic problem has two stable periodic orbits separated by the switching manifold \(\Sigma=\{(t,x)\in \mathbb{R}^+\times \mathbb{R}: x=0\}\).
In the figure below we illustrate a contour plot of the probability of such tipping events overlaid on the deterministic dynamics. The curves \(\Sigma_A\) and \(\Sigma_R\) correspond to deterministic attracting and repelling sliding regions on \(\Sigma\). The solid red and blue curves are deterministic stable limit cycles while the green curve is the unstable limit cycle seperating the two. It is interesting to note that realizations of the noise that transition from the lower to upper stable limit cycle with overwhelming probability seem to track the switching manifold well outside of \(\Sigma_A\). Jessi's thesis work and subsequent research has been devoted to understanding this phenomenon. 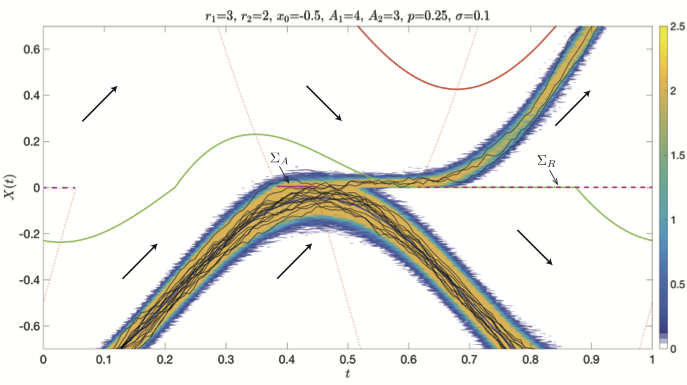
The specific tool Jessi has been using in her work is the so called "path integral formulation". That is, in the limit of vanishing noise strength, i.e. (\(\sigma\rightarrow 0\)), most probable tipping events connecting a point \((t_0,x_0)\) on the stable lower limit cycle to the upper stable limit cycle \((t_f,x_f)\) are taken to be minimizers of the following Onsager-Machlup functional: \[I[x]=\int_{t_0}^{t_f} (\dot{x}-f(x(t),t))^2dt+\frac{\sigma^2}{2}\int_{t_0}^{t_f} f_x(x(t),t)dt.\] However, since \(f(x,t)\) is not smooth for our system it is not clear that this approach is valid. Jessi has been instead considering a smoothed out version of the drift and studying minimizers of the Onsager-Machlup functional in the limit in which the charcteristic length scale set by the smoothing vanishes. In the figures below Jessi's results are compared with Monte-Carlo simulations. The solid black curves correspond to most probable tipping events that Jessi numerically computed by applying a gradient flow to the smoothed out version of the Onsager-Machlup functional. It is interesting to note that Jessi's numerics clearly predict sliding like behavior of the tipping events for particular parameter regimes. This sliding behavior is closely linked with the geometry of the flow on either side of the switching region. Jessi and I are currently colloborating on understanding how this sliding behavior can be rigorously understood in the limit in which the noise strength and smoothing parameter vanish.
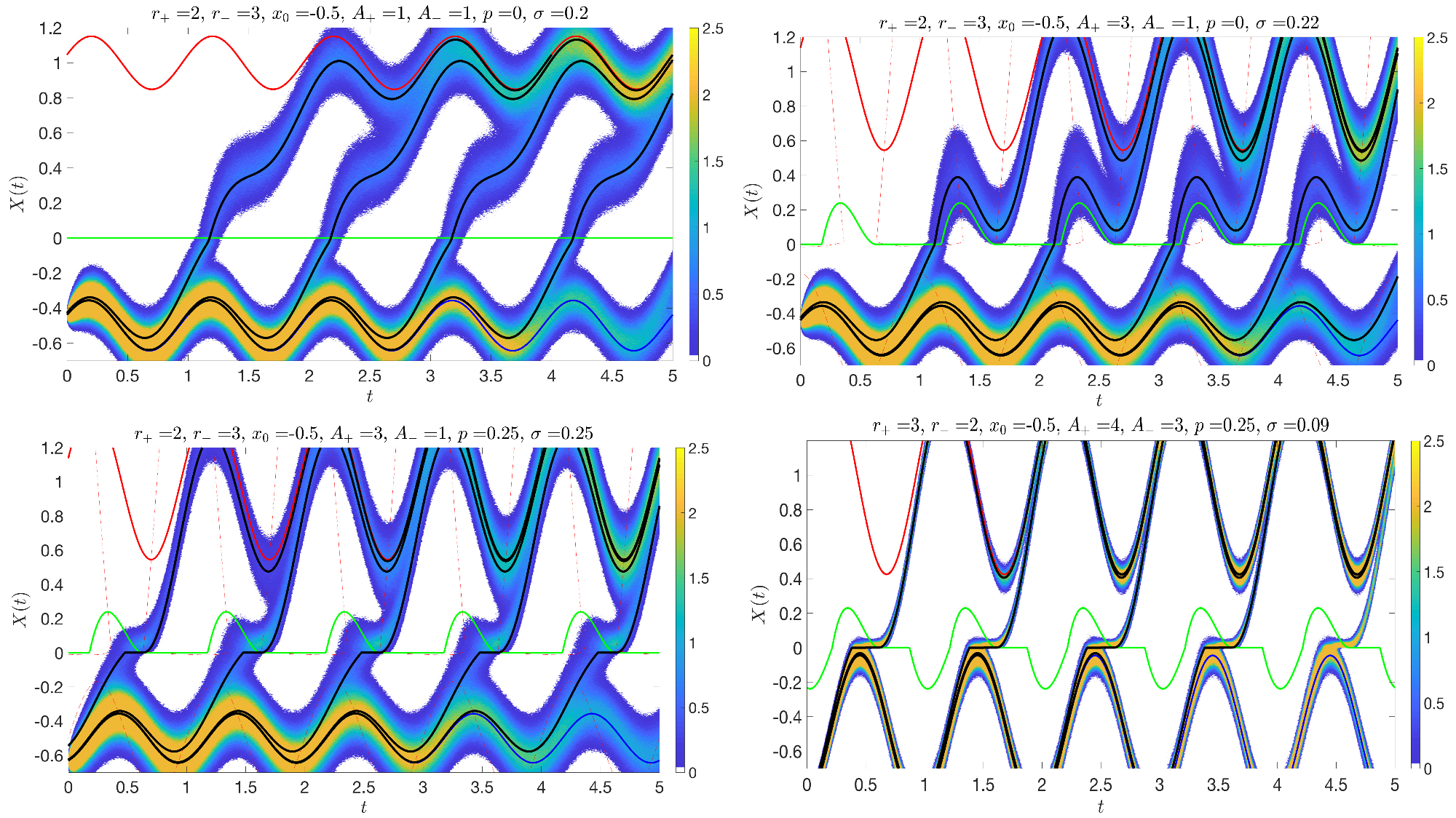
In the figure below we illustrate a contour plot of the probability of such tipping events overlaid on the deterministic dynamics. The curves \(\Sigma_A\) and \(\Sigma_R\) correspond to deterministic attracting and repelling sliding regions on \(\Sigma\). The solid red and blue curves are deterministic stable limit cycles while the green curve is the unstable limit cycle seperating the two. It is interesting to note that realizations of the noise that transition from the lower to upper stable limit cycle with overwhelming probability seem to track the switching manifold well outside of \(\Sigma_A\). Jessi's thesis work and subsequent research has been devoted to understanding this phenomenon.

The specific tool Jessi has been using in her work is the so called "path integral formulation". That is, in the limit of vanishing noise strength, i.e. (\(\sigma\rightarrow 0\)), most probable tipping events connecting a point \((t_0,x_0)\) on the stable lower limit cycle to the upper stable limit cycle \((t_f,x_f)\) are taken to be minimizers of the following Onsager-Machlup functional: \[I[x]=\int_{t_0}^{t_f} (\dot{x}-f(x(t),t))^2dt+\frac{\sigma^2}{2}\int_{t_0}^{t_f} f_x(x(t),t)dt.\] However, since \(f(x,t)\) is not smooth for our system it is not clear that this approach is valid. Jessi has been instead considering a smoothed out version of the drift and studying minimizers of the Onsager-Machlup functional in the limit in which the charcteristic length scale set by the smoothing vanishes. In the figures below Jessi's results are compared with Monte-Carlo simulations. The solid black curves correspond to most probable tipping events that Jessi numerically computed by applying a gradient flow to the smoothed out version of the Onsager-Machlup functional. It is interesting to note that Jessi's numerics clearly predict sliding like behavior of the tipping events for particular parameter regimes. This sliding behavior is closely linked with the geometry of the flow on either side of the switching region. Jessi and I are currently colloborating on understanding how this sliding behavior can be rigorously understood in the limit in which the noise strength and smoothing parameter vanish.

