Phase Shaping of Beams
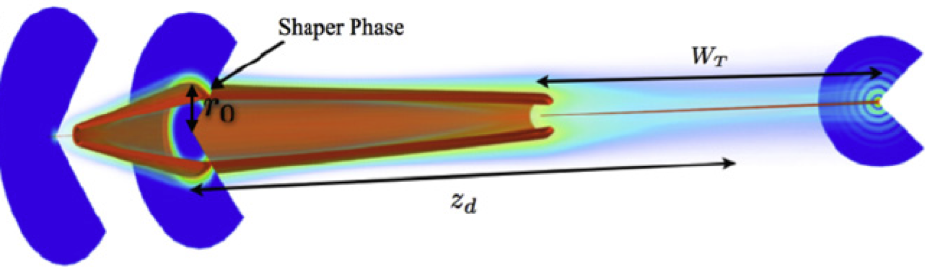
In many applications it is desirable to shape a beam or pulse of light so that it has specific properties along the optical axis. In particular, for applications in microscopic imaging, optical tweezers, laser micro-machining, dressing of optical filaments, filament formation and long-range laser ablation, to name a few, it is important to have a well controlled beam with a nearly uniform intensity along the optical axis. However, due to its wave nature localized packets of light will broaden spatially through diffraction. For example, Gaussian beams of width \(W_0\) and wavenumber \(k\) double in spatial extent over the Rayleigh range \(z_R\sim W_0^2k/2\). In collaboration with Charles Durfee an experimental physicist at the Colorado School of Mines and mathematicians Jerome Moloney at the University of Arizona and Shankar Venkataramani I have studied the problem of phase shaping beams of light into desired intensity profiles. Our research was focused on ``beating'' the Rayleigh range by applying a radially symmetric phase function \(\phi(r)\) at the input plane \(z=0\) to focus a ring beam intensity profile \(E_0f(r)\) of radius \(r_0\) and width \(W_0\) onto a target intensity profile \(E_TF_T(z)\) of width \(W_T\) along the optical axis centered at a target distance \(z_d\); see the below figure.
Mathematical model:
In our work we reformulated this optical design problem in terms of a minimization problem for the following functional: \[ I[\varphi]=\|G(\Omega)-|\mathcal{F}[g(s)\exp\left(i \varphi(s)\right)](\Omega)|\, \|_{L^2}, \] where \(g\) and \(G\) are given positive compactly supported functions, \(\mathcal{F}\) denotes the Fourier transform and the minimization is over the space \(\mathcal{M}\) of measurable functions on \(\mathbb{R}^+\). This problem is closely related to the problem of phase retrieval from two intensity measurements, i.e. the problem of determining the complex argument of a function given both knowledge of the modulus of a function and the modulus of its Fourier transform. Within the context of phase retrieval, the most common technique for optimizing \(I\) is the alternating projection algorithm pioneered by Gerchberg and Saxton and its variants such as the hybrid input-output algorithm discovered by Fienup. In the original Gerchberg-Saxton (GS) algorithm the phase is recovered as follows:
Through Plancherel's indentity it can be shown that the GS algorithm is an error reducing algorithm in the sense that \(I[\varphi_{n+1}]\leq I[\varphi_n]\). However, this property alone does not guarantee convergence of the algorithm. In particular, while projection algorithms converge when the projections are onto convex sets, for fixed \(s\) or \(\Omega\) the projections employed by the GS algorithm are equivalent to projections onto the boundary of the unit ball in \(\mathbb{C}\) which is clearly not convex. This lack of convexity commonly leads to stagnation of the algorithm away from the global minimum which must be overcome by additional ad hoc means. However, while in phase retrieval it is clear that the minimum value is zero, for the optimization problem we considered this is not the case and in fact the minimum may be significantly bounded away from zero. Therefore, when applied to this variational problem it is not clear a priori what a sufficient convergence criterion for the GS algorithm would be.
Method of stationary phase:
We developed an adapted version of the GS algorithm to avoid this stagnation issue. Namely, we used the method of stationary to construct a phase \(\phi\) that satisfies \(\lim_{k\rightarrow \infty} I[\phi]=0\). The phase is constructed as follows:
Uncertainty principle:
Moreover, using essentially the uncertainty principle we proved ansatz free lower bounds on the minimum value of this functional which quantify that a necessary condition for accurate beam shaping is that \[ \beta=\frac{2kW_TW_0r_0}{4z_d^2-W_T^2}>\pi. \] The central result of our work is the identification of the dimensionless quantity \(\beta\)'s critical role in determining the accuracy and applicability of phase shaping in term of the design parameters. Namely, we identified three scaling regimes:
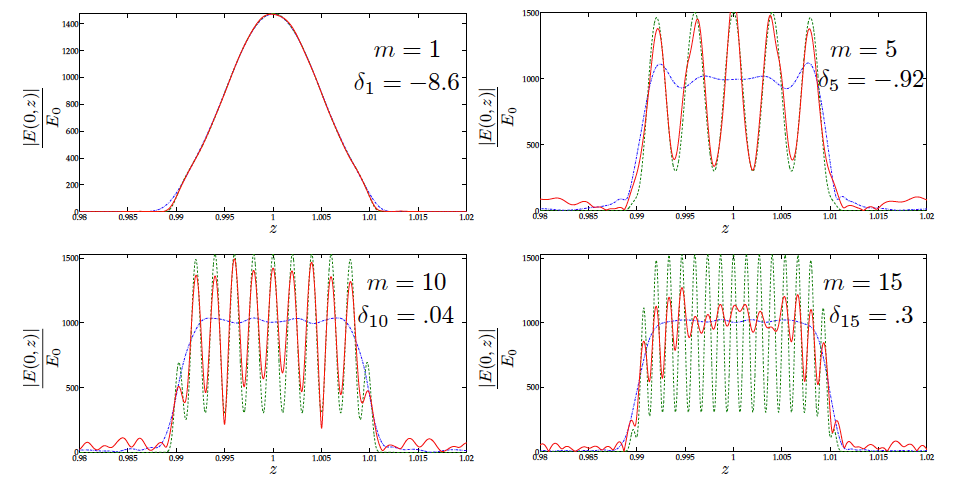
The figure below illustrates our theory in practice. The dashed green curve is the target profile, blue the intensity profile generated by the stationary phase ansatz, red the result of using the GS algorithm with our stationary phase ansatz as the initial guess. The value \(\delta\) is a local measure of \(\beta\) and for positive values our theory predicts that phase shaping will do a poor job of matching the target intensity. In particular, phase shaping is unable to resolve the small scale features in the target intensity profile.
Outlook:
Our work has primarly been concerened with phase shaping the linear optical regime. For more realistic implementations it is necessary to consider the role that turbulence plays in the phase shaping and how additional techniques such as adaptive optics can be deployed to compensate for atmospheric effects. Additionaly, a natural next step would be to consider optical nonlinearities such as the Kerr effect.
References:

Mathematical model:
In our work we reformulated this optical design problem in terms of a minimization problem for the following functional: \[ I[\varphi]=\|G(\Omega)-|\mathcal{F}[g(s)\exp\left(i \varphi(s)\right)](\Omega)|\, \|_{L^2}, \] where \(g\) and \(G\) are given positive compactly supported functions, \(\mathcal{F}\) denotes the Fourier transform and the minimization is over the space \(\mathcal{M}\) of measurable functions on \(\mathbb{R}^+\). This problem is closely related to the problem of phase retrieval from two intensity measurements, i.e. the problem of determining the complex argument of a function given both knowledge of the modulus of a function and the modulus of its Fourier transform. Within the context of phase retrieval, the most common technique for optimizing \(I\) is the alternating projection algorithm pioneered by Gerchberg and Saxton and its variants such as the hybrid input-output algorithm discovered by Fienup. In the original Gerchberg-Saxton (GS) algorithm the phase is recovered as follows:
- Choose an initial guess \(\varphi_0 \in \mathcal{M}\).
- Define \(\Psi_n=\arg\left(\mathcal{F}\left[g(s)\exp\left(i \varphi_{n-1}(s)\right)\right]\right)\).
- Define \(\varphi_n=\arg\left(\mathcal{F}^{-1}\left[G(\Omega)\exp\left(\left(i \Psi_n(\Omega)\right)\right)\right]\right)\).
- Loop through items 2 and 3 until \(I[\varphi_n]\) is sufficiently close to zero.
Through Plancherel's indentity it can be shown that the GS algorithm is an error reducing algorithm in the sense that \(I[\varphi_{n+1}]\leq I[\varphi_n]\). However, this property alone does not guarantee convergence of the algorithm. In particular, while projection algorithms converge when the projections are onto convex sets, for fixed \(s\) or \(\Omega\) the projections employed by the GS algorithm are equivalent to projections onto the boundary of the unit ball in \(\mathbb{C}\) which is clearly not convex. This lack of convexity commonly leads to stagnation of the algorithm away from the global minimum which must be overcome by additional ad hoc means. However, while in phase retrieval it is clear that the minimum value is zero, for the optimization problem we considered this is not the case and in fact the minimum may be significantly bounded away from zero. Therefore, when applied to this variational problem it is not clear a priori what a sufficient convergence criterion for the GS algorithm would be.
Method of stationary phase:
We developed an adapted version of the GS algorithm to avoid this stagnation issue. Namely, we used the method of stationary to construct a phase \(\phi\) that satisfies \(\lim_{k\rightarrow \infty} I[\phi]=0\). The phase is constructed as follows:
- The following initial value problem is solved: \[ \begin{cases} \displaystyle{\frac{dz_c}{d\rho}=2\pi k \frac{E_0^2 f(\rho)}{E_T^2 F_T^2(z_c(\rho))} \rho}\\ z_c\left(r_0-\frac{W_0}{2}\right)=z_d-\frac{W_T}{2} \end{cases}. \]
- The phase is found by integrating: \[ \phi(\rho)=-k \int_{r_0-\frac{W_0}{2}}^{\rho} \frac{u}{z_c(u)}\,du. \]
Uncertainty principle:
Moreover, using essentially the uncertainty principle we proved ansatz free lower bounds on the minimum value of this functional which quantify that a necessary condition for accurate beam shaping is that \[ \beta=\frac{2kW_TW_0r_0}{4z_d^2-W_T^2}>\pi. \] The central result of our work is the identification of the dimensionless quantity \(\beta\)'s critical role in determining the accuracy and applicability of phase shaping in term of the design parameters. Namely, we identified three scaling regimes:
- For \(\beta \ll \pi\) the uncertainty principle guarantees that the GS algorithm nor any other numerical algorithm will yield accurate shaping of the beam.
- For \(\beta \gg \pi\) the method of stationary phase yields a very accurate approximation to the optimal shaper phase. This asymptotic regime can be considered within the geometrical optics setting in the sense that light rays originating from the input plane are accurately mapped to the target intensity profile.
- For \(\beta \sim \pi\) the phase produced by the method of stationary phase is significantly improved upon by the GS algorithm. However, a universal scaling law for the error in terms of the wavelength is not possible.
The figure below illustrates our theory in practice. The dashed green curve is the target profile, blue the intensity profile generated by the stationary phase ansatz, red the result of using the GS algorithm with our stationary phase ansatz as the initial guess. The value \(\delta\) is a local measure of \(\beta\) and for positive values our theory predicts that phase shaping will do a poor job of matching the target intensity. In particular, phase shaping is unable to resolve the small scale features in the target intensity profile.

Outlook:
Our work has primarly been concerened with phase shaping the linear optical regime. For more realistic implementations it is necessary to consider the role that turbulence plays in the phase shaping and how additional techniques such as adaptive optics can be deployed to compensate for atmospheric effects. Additionaly, a natural next step would be to consider optical nonlinearities such as the Kerr effect.
References:
- Durfee, C. G., Gemmer, J., Moloney, J. V. (2013). Phase-only shaping algorithm for Gaussian-apodized Bessel beams. Optics express, 21(13), 15777-15786.
- Gemmer, J. A., Venkataramani, S. C., Durfee, C. G., Moloney, J. V. (2014). Optical beam shaping and diffraction free waves: A variational approach. Physica D: Nonlinear Phenomena, 283, 15-28.
