John A. Gemmer

Mathematically, swelling can be modeled by a Riemannian metric \[\mathbf{g} = g_{11}(x, y)dx^2 + 2g_{12}(x, y)dxdy + g_{22}(x, y)dy^2\] that encodes how the intrinsic distance between material coordinates changes during the swelling process. The equilibrium configuration is then taken to be a sufficiently smooth deformation \(\mathbf{x} : \mathcal{D}\rightarrow \mathbb{R}^3\) that minimizes a non-Euclidean Foppl - von Karman energy: \[\mathcal{E}[\mathbf{x}]=\underbrace{\int_{\mathcal{D}}\|\nabla \mathbf{x}^T\cdot \nabla \mathbf{x}-\mathbf{g}\|^2\,dA}_{0 \text{ for isometries}}+\underbrace{t^2\int_{\mathcal{D}}(k_1^2+k_2^2)\,dA}_{0 \text{ for flat surfaces}}\] where \(\mathcal{D}\) is the midsurface of the undeformed sheet, \(t\) is the thickness of the sheet and \(k_1, k_2\) are the principal curvatures of the deformed surface. The term \(\nabla \mathbf{x}^T \cdot \nabla \mathbf{x} − \mathbf{g}\) measures in-plane strain caused by stretching and vanishes when the surface is an isometric immersion of \(g\), i.e. a solution of the equation \(\nabla \mathbf{x}^T \cdot \nabla \mathbf{x} = \mathbf{g}\), while \(k_1^2+k_2^2\) measures the local bending of the surface. For metrics with non-zero Gaussian curvature the bending and stretching terms cannot both vanish globally and the competition between these two energies sets the equilibrium configuration. Specifically, in the vanishing thickness limit the stretching energy is dominant and minimizers converge to a shape that minimizes the bending energy over all possible isometric immersions. This type of specified morphogenesis is being explored as a technique for creating desired three dimensional structures. The advantage of this technique over direct casting is that the process is reversible and can be used to create "soft machines" such as actuators, valves, and pumps. The mathematics I am working on will allow these structures to be realized by accurately predicting equilibrium shapes from swelling data.

Constant Gaussian Curvature:

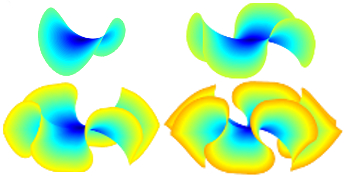
In references [1-4] we studied the problem of constructing and analyzing the bending energy for isometric immersions of \(\mathbb{H}^2\) into \(\mathbb{R}^3\). We were motivated by experiments on hydrogel disks with programmed constant Gaussian curvature. With decreasing thickness these hydrogels adopted a saddle shape that transitioned to multi-wave shapes with decreasing thickness; see the figure to the below left. Motivated by these experimental results, in [1] we constructed \(W^{2,2}\) isometric immersions of \(\mathbb{H}^2\) with periodic profiles that qualitatively these experimentally realized shapes; see the lower right figure. We showed that for purely geometrical reasons, the number of waves in these isometric immersions must refine with increasing radius matching observations in crochet models of \(\mathbb{H}^2\). Indeed, we provided strong numerical evidence that for large radii these periodic shapes are energetically preferred over saddle shapes; see Fig. 1. However, in [4] we rigorously proved by finding ansatz free scaling laws that for the range of parameters used in these experiments the global minimizers of the variational problem are the saddle shapes for all thickness values.


In [1] we show that the self-similar shapes observed in torn plastic can be explained by low energy piecewise smooth isometric immersions.

More information on my work in this area can be found in the publications listed below.

Video of a presentation given at the IMA

Publications Related to this Work:

1. Gemmer, J. A., & Venkataramani, S. C. (2011). Shape selection in non-Euclidean plates. Physica D: Nonlinear Phenomena, 240(19), 1536-1552.
2. Gemmer, J. (2012). Shape Selection in the non-Euclidean Model of Elasticity (Doctoral dissertation, The University Of Arizona).
3. Gemmer, J. A., & Venkataramani, S. C. (2012). Defects and boundary layers in non-Euclidean plates. Nonlinearity, 25(12), 3553.
4. Gemmer, J. A., & Venkataramani, S. C. (2013). Shape transitions in hyperbolic non-Euclidean plates. Soft Matter, 9(34), 8151-8161
5. Gemmer, J. A., Venkataramani, S. C., Sharon, E. (2016) Isometric immersions and self-similar buckling in Non-Euclidean elastic sheets. (preprint).

Potential Graduate Student Research:

So far my work has focused on studying swelling thin elastic sheets with a specific swelling pattern, namely one whose geometry corresponds to constant negative Gaussian curvature. I believe that the results I have in the case of constant Gaussian curvature will still hold for more generic swelling patterns. One way a student could assist me is by designing, running, and analyzing numerical simulations of swelling thin elastic sheets with generic radially symmetric swelling patterns. This project could be undertaken by a student with experience in differential equations, numerical analysis,  and programming in a higher level language like Mathematica of Matlab. The essential question the student will be exploring is the role of geometry in determining complex morphologies observed in leaves and torn plastic. I believe that this project could nucleate into further research that would have a high impact on the field.

Another project that could be pursued by a graduate student is to develop and analyze a mathematical of swelling thin elastic sheets that incorporates dynamic and stochastic effects. My past work has shown that local but not global minimum seem to be what is observed in practice. This project could be undertaken by a student with experience in differential equations, numerical analysis, elasticity, calculus of variations and programming in a higher level language like Mathematica of Matlab. This research could serve as the beginning of a Ph.D. dissertation.