Isometric Immersions of \( \mathbb{H}^2 \)
In references [1-4] I studied in collaboration with Shankar Venkataramani the problem of minimizing the bending energy of isometric immersions of \(\mathbb{H}^2\) into \(\mathbb{R}^3\). That is for \(\Omega \subset \mathbb{R}^2\) a smooth, simply connected domain and \(\mathcal{A}=\{\mathbf{x}\in W^{2,2}(\Omega;\mathbb{R}^3):\nabla \mathbf{x}^T\cdot \nabla \mathbf{x}=\mathbf{g}_{\mathbb{H}^2}\} \) we were interesting in minimizing the functional \(\mathcal{B}: \mathcal{A}\mapsto \mathbb{R}\) defined by \[\mathcal{B}[\mathbf{x}]=\int_{\Omega}\left(k_1^2+k_2^2\right)\,dxdy,\] where \(k_1\) and \(k_2\) are the principal curvatures of the sheet. This bending energy is a proxy for the elastic energy of a growing sheet that matches a specific Riemannian geometry, in this case constant negative Gaussian curvature \(K_0\).
Exact isometries:
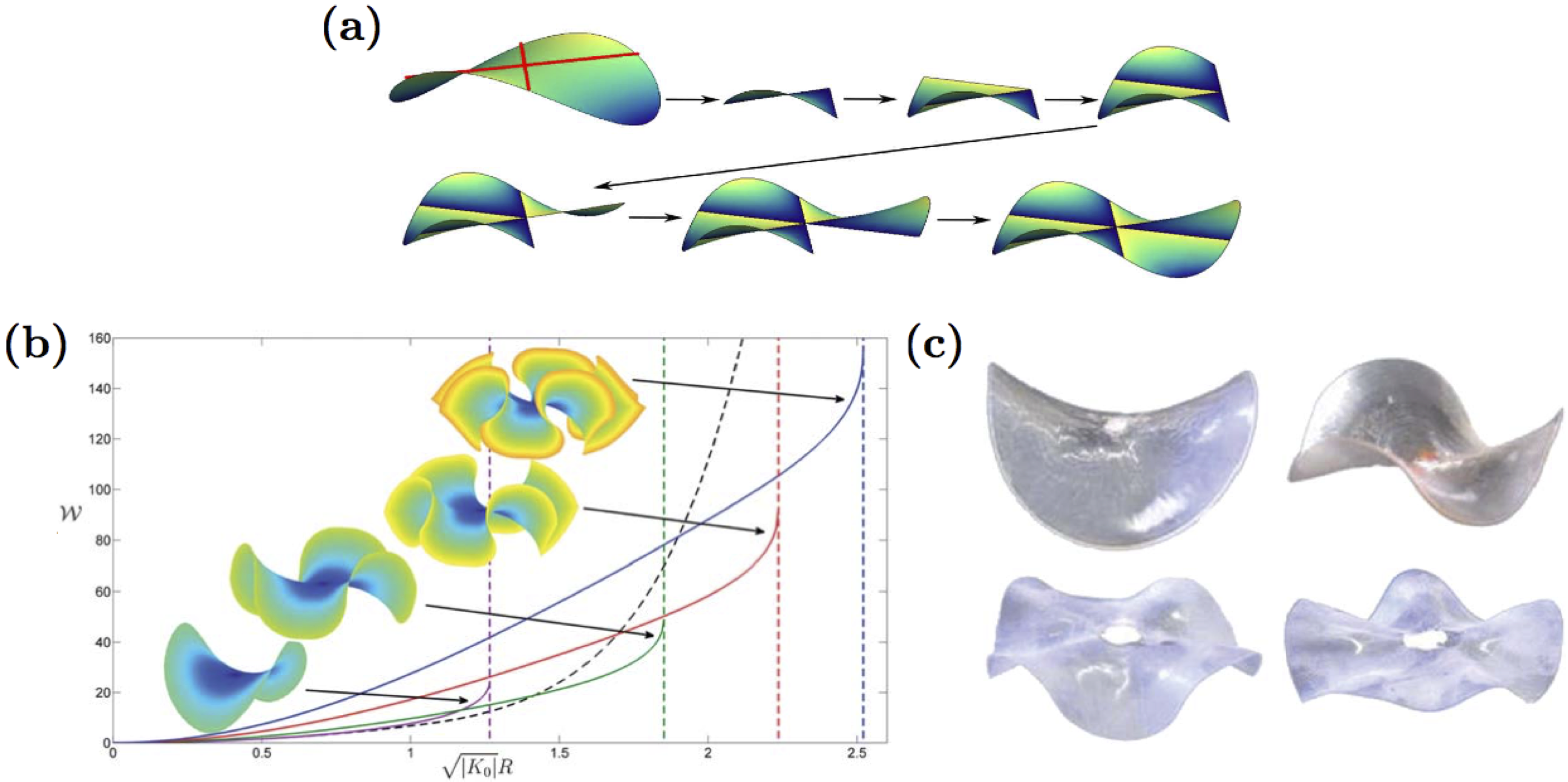
Our work on this problem was motivated by experiments on hydrogel disks with programmed constant Gaussian curvature. With decreasing thickness these hydrogels adopted a saddle shape that transitioned to multi-wave shapes with decreasing thickness; see Fig (c) below. In this setting the problem of studying the elastic energy of isometric immersions reduces to analyzing the behavior of solutions to the sine-Gordon equation: \[\frac{\partial^2 \phi}{\partial x \partial y} =-K_0\sin(\phi),\] where \(\phi\) is restricted to lie in the set \([0,\pi]\) is the angle between coordinate curves in a Chebychev net (C-net) parametrization. By considering smooth solutions to the sine-Gordon equation we provided strong numerical evidence that the principal curvatures of smooth isometric immersions satisfy the following scaling law: \begin{equation} \max\{|k_1|,|k_2|\} \geq \frac{1}{64} \exp\left( |K_0|^{\frac{1}{2}}R\right), \end{equation} where \(R\) is the diameter of the domain. This scaling law emphasizes that with increasing domain size it becomes prohibitively expensive to maintain smoothness and the isometry constraint.
By explicit construction we showed that an energetically favorable alternative is for the sheet to introduce mild singularities in the form of lines of inflection to obtain \(n\)-periodic "monkey saddles". Specifically, these isometries are formed by solving the sine-Gordon equation with boundary conditions that enforce the C-net parameterization to contain two straight asymptotic lines that intersect at the origin. By taking odd periodic reflections about these lines the monkey saddles can be constructed; see Fig. Fig (a) below. These monkey saddles are not smooth -- every smooth isometry locally has the shape of a saddle -- but nevertheless are finite bending energy isometric immersions, i.e. \(W^{2,2}\) isometric immersions. In particular, as illustrated in Fig (b) below, for moderate domain sizes these isometries have lower elastic energy than their smooth counterparts. Moreover, these shapes qualitatively agree with the experiments on hydrogels with constant Gaussian curvature.
Small slope approximation:
Our exact construction of these isometric immersions does not, however, entirely explain the phenomenon observed in experiments. We also explored with the small-slope approximation the effect of stretching. Namely, defining the small parameter \(\epsilon=\sqrt{|K_0|}R\) we assumed an in-plane and out-of-plane ansatz of the form \[ F=i+\sqrt{K_0}i_{\perp} \circ \eta +K_0i \circ \chi,\] where \(\chi \in W^{1,2}(\Omega; \mathbb{R}^2)\), \(\eta\in W^{2,2}(\Omega;\mathbb{R})\), \(i:\mathbb{R}^2\mapsto \mathbb{R}^3\) is the standard immersion and \(i_{\perp}\) maps into the orthogonal compliment of \(i(\mathbb{R}^2)\). Keeping terms only up to order \(\epsilon^2\) the solvability condition for the existence of an isometric immersion is the following Monge-Ampere equation: \[ \det(D^2 \eta)=-1.\] This equation can be solved explicitly by assuming \(\eta=ax^2+bxy+cy^2\) which reduces the differential equation to the simple algebraic equation \(4ac-b^2=-1\). The global minimum of the elastic energy is obtained by the harmonic function \(\eta=xy\) which corresponds to a minimal surface within the small-slope approximation. As above, \(n\)-wave monkey saddle solutions to the Monge-Ampre equation can also be constructed by introducing lines of inflection and taking odd periodic reflections. However, using a priori estimates we proved that the full elastic energy including the stretching energy obeys the following scaling law \[ c n t^2\leq \inf E[F]\leq Cn^2 t^2 \label{Eq:SmSlopeScaling} \] in the small-slope regime. This result quantifies the tradeoff in energy that occurs by increasing the number of waves in the profile and proves that in the small-slope regime there can be no refinement of the wavelength of minimizers with decreasing thickness.
Outlook:
At first glance our mathematical results and experimentally observed phenemenon appear to contradict each other. However, our mathematical constructions are local minimum for this variational problem. Our results indicate that this is a "floppy" system in that there are many local minimum seperated by very small energy barriers. Such a system is consequently susceptible to small changes in the system. In particular neglected phenomenon such as gravity, line tension, thermal flucations, viscoelastic effects, etc. might cause the system to select local minimum. Our exact constructions of local minimum are natural starting points to consider what patterns are selected by such additional effects.
References:
Exact isometries:
Our work on this problem was motivated by experiments on hydrogel disks with programmed constant Gaussian curvature. With decreasing thickness these hydrogels adopted a saddle shape that transitioned to multi-wave shapes with decreasing thickness; see Fig (c) below. In this setting the problem of studying the elastic energy of isometric immersions reduces to analyzing the behavior of solutions to the sine-Gordon equation: \[\frac{\partial^2 \phi}{\partial x \partial y} =-K_0\sin(\phi),\] where \(\phi\) is restricted to lie in the set \([0,\pi]\) is the angle between coordinate curves in a Chebychev net (C-net) parametrization. By considering smooth solutions to the sine-Gordon equation we provided strong numerical evidence that the principal curvatures of smooth isometric immersions satisfy the following scaling law: \begin{equation} \max\{|k_1|,|k_2|\} \geq \frac{1}{64} \exp\left( |K_0|^{\frac{1}{2}}R\right), \end{equation} where \(R\) is the diameter of the domain. This scaling law emphasizes that with increasing domain size it becomes prohibitively expensive to maintain smoothness and the isometry constraint.
By explicit construction we showed that an energetically favorable alternative is for the sheet to introduce mild singularities in the form of lines of inflection to obtain \(n\)-periodic "monkey saddles". Specifically, these isometries are formed by solving the sine-Gordon equation with boundary conditions that enforce the C-net parameterization to contain two straight asymptotic lines that intersect at the origin. By taking odd periodic reflections about these lines the monkey saddles can be constructed; see Fig. Fig (a) below. These monkey saddles are not smooth -- every smooth isometry locally has the shape of a saddle -- but nevertheless are finite bending energy isometric immersions, i.e. \(W^{2,2}\) isometric immersions. In particular, as illustrated in Fig (b) below, for moderate domain sizes these isometries have lower elastic energy than their smooth counterparts. Moreover, these shapes qualitatively agree with the experiments on hydrogels with constant Gaussian curvature.

Small slope approximation:
Our exact construction of these isometric immersions does not, however, entirely explain the phenomenon observed in experiments. We also explored with the small-slope approximation the effect of stretching. Namely, defining the small parameter \(\epsilon=\sqrt{|K_0|}R\) we assumed an in-plane and out-of-plane ansatz of the form \[ F=i+\sqrt{K_0}i_{\perp} \circ \eta +K_0i \circ \chi,\] where \(\chi \in W^{1,2}(\Omega; \mathbb{R}^2)\), \(\eta\in W^{2,2}(\Omega;\mathbb{R})\), \(i:\mathbb{R}^2\mapsto \mathbb{R}^3\) is the standard immersion and \(i_{\perp}\) maps into the orthogonal compliment of \(i(\mathbb{R}^2)\). Keeping terms only up to order \(\epsilon^2\) the solvability condition for the existence of an isometric immersion is the following Monge-Ampere equation: \[ \det(D^2 \eta)=-1.\] This equation can be solved explicitly by assuming \(\eta=ax^2+bxy+cy^2\) which reduces the differential equation to the simple algebraic equation \(4ac-b^2=-1\). The global minimum of the elastic energy is obtained by the harmonic function \(\eta=xy\) which corresponds to a minimal surface within the small-slope approximation. As above, \(n\)-wave monkey saddle solutions to the Monge-Ampre equation can also be constructed by introducing lines of inflection and taking odd periodic reflections. However, using a priori estimates we proved that the full elastic energy including the stretching energy obeys the following scaling law \[ c n t^2\leq \inf E[F]\leq Cn^2 t^2 \label{Eq:SmSlopeScaling} \] in the small-slope regime. This result quantifies the tradeoff in energy that occurs by increasing the number of waves in the profile and proves that in the small-slope regime there can be no refinement of the wavelength of minimizers with decreasing thickness.
Outlook:
At first glance our mathematical results and experimentally observed phenemenon appear to contradict each other. However, our mathematical constructions are local minimum for this variational problem. Our results indicate that this is a "floppy" system in that there are many local minimum seperated by very small energy barriers. Such a system is consequently susceptible to small changes in the system. In particular neglected phenomenon such as gravity, line tension, thermal flucations, viscoelastic effects, etc. might cause the system to select local minimum. Our exact constructions of local minimum are natural starting points to consider what patterns are selected by such additional effects.
References:
- Gemmer, J. A., & Venkataramani, S. C. (2011). Shape selection in non-Euclidean plates. Physica D: Nonlinear Phenomena , 240(19), 1536-1552.
- Gemmer, J. (2012). Shape Selection in the non-Euclidean Model of Elasticity (Doctoral dissertation, The University Of Arizona).
- Gemmer, J. A., & Venkataramani, S. C. (2012). Defects and boundary layers in non-Euclidean plates. Nonlinearity, 25(12), 3553.
- Gemmer, J. A., & Venkataramani, S. C. (2013). Shape transitions in hyperbolic non-Euclidean plates. Soft Matter, 9(34), 8151-8161
