Direction Selectivity on the Retina
It is fascinating to me that many animals can maintain a stable image when moving. For example, when an athlete tracks a ball they can lock onto the image and keep it steady as they run. In contrast, when we try to record a movie by simply holding a camera we often get the "shaken camera" effect. As an aside, here is a link to - in my opinion - a very amusing commerical illustrating how chickens are naturally adept at stabilizaing their field of view (note: I do not endorse nor do I receive any funding from LG). It is an interesting question how the brain, eyes and muscles in an animal can respond quickly to stabilize an image.
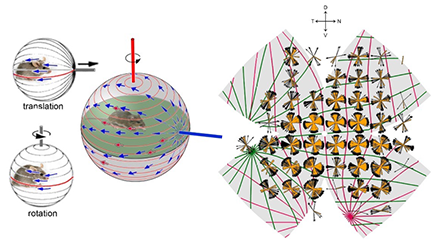
Now, it is well known that when animals move, visual and vestibular signals inform the brain which drives postural adjustments, image-stabilizing eye and head movements, and cerebellar learning. It is also well known that otolithic organs (saccule and utricle) encode translation along axes in specific planes, while semicircular canals encode rotation about one of three axes. Geometrically, vestibular planes and axes are orthogonal so that the relative activation of vestibular channels uniquely encodes any possible translation or rotation. On the other hand, when the animal is still moving objects generate "optic flow", the global pattern of retinal image motion. When translating, optic flow diverges from a point in extrapersonal space (the ‘direction of heading’) and converges at a diametrically opposed singularity, see the below image. Features in the animal’s global visual space move along arcs of longitude (meridians) originating from these singularities or poles. When rotating, optic flow circulates around an axis along lines of latitude or, in projection, around a point in visual or retinal space. Rotational and translational optic flow evoke different behaviors, implying divergent encoding mechanisms. Neurons encoding local movement direction are well-known in the eye and brain. Some brain neurons encode global optic flow, but little is known about how these are constructed from retinal inputs and how this relates to the vestibular representation of self-motion. Retinal direction-selective ganglion cells (DSGCs) are neurons on the retina that respond to optic flow aligned in preferred directions. It is believed that DSGCs belong to two classes, the ON and ON-OFF-DSGCs which differ in structure, projections, physiological properties, and functional roles. ON-OFF-DSGCs are further divisible into four subtypes based on preferred direction. They feed retinotopically organized brainstem and cortical centers mediating gaze shifts and conscious motion perception. In contrast, ON DSGCs comprise three subtypes and innervate the accessory optic system (AOS). The AOS encodes rotational optic flow around the best axes of the semicircular canals to mediate image-stabilizing optokinetic reflexes.
In collaboration with biologists David Berson and Shai Sabbah at Brown University I have developed and analyzed a mathematical model of how retinal ganglion cells encode the direction and spatial orientation of perceived objects moving in space. Namely, I developed an elastic model of flat mounted retinas that has been used to relate in-vitro measurements of cell response with in-vivo response of external stimulus. The mathematical model I developed allowed us to understand how the accessory optic system within the brain assembles and compares signals generated by translational and rotational optic flow. The rightmost image below qualitatively compares the measured optic flow with optic flow generated from our models. Namely, the green and red curves are the translational optic flows that are best correlated with our data when mapped to a computational reconstructed retina.
Mathematical model:
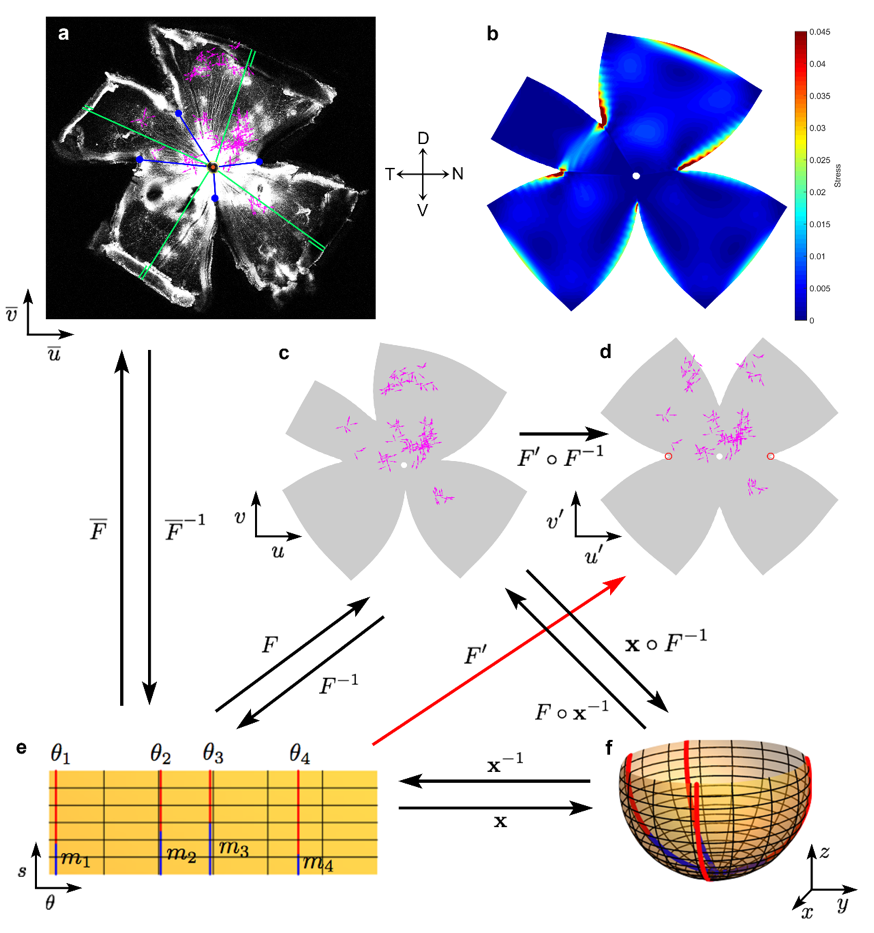
My primary role in this project was to develop a mathematical model for reconstructing the retina from measurments of a flat mounted retina. This is essentially like trying to construct an orange from information about the shapes of its peels. Specifically, I modeled the retina as a spherical object \(\mathcal{S}\) of radius \(R\) and maximal longitudinal distance \(M\) with four cuts made along lines of longitude. The retina was parametrized with domain of parametrization \(\mathcal{D}\) by arc length \(s\) as measured from the south pole and \(\theta\) the azimuthal angle. The flattening of the retina was modeled by a mapping \(F:\mathcal{D}\mapsto \mathcal{D}^{\prime} \subset \mathbb{R}^2\) that minimizes an appropriate elastic energy. Specifically, we assumed the retina is an isotropic elastic material with linear stress-strain constitutive relationship and model the per-unit thickness elastic energy of a flattening map \(F\in W^{1,4}(\mathcal{D},\mathcal{D}^{\prime})\) by \[ E[F]=\sum_{i=1}^{4} \int_{\mathcal{D}_i} \left[ \nu\left(\gamma_{11}+\gamma_{22}\right)^2+(1-\nu)\left(\gamma_{11}^2+2\gamma_{12}^2+\gamma_{22}^2\right)\right]\sin\left(\frac{s}{R}\right)ds d\theta,\] where \(\nu\) is the Poisson ratio for the material, \(\gamma_{ij}\) the intrinsic in-plane strain tensor accounting for the curvature of the sphere, and the summation is over each sector of the retina as defined by the cuts. Optimization of this energy was performed using a Rayleigh-Ritz type algorithm. This computational model allowed us to record data from a number of flat mounted retinas and combine it onto a computationally constructed "standard retina".
The diagram below illustrates the various coordinate systems and mapping used to computational reconstruct the retina. (a) Example confocal image of a retina from one experiment. Four radial relieving cuts were made in the eyecup to facilitate flattening, with termini indicated by blue circles. Each magenta vector represents the location and DS preference of a single DSGC. (b) Strain energy density estimating regions of local stretching resulting from the flattening process of the retina. (c-f) Remapping of DSGC locations onto a standardized spherical retinal coordinate system for pooling data across experiments and permitting display in flattened (c,d) or projected spherical form (f). c. Retina in (a) after mapping in standardized spherical coordinates, followed by remapping into flattened form using modeled relieving cuts approximating the actual ones; close similarity to (a) indicates the faithfulness and reversibility of these transformations. (d) Same as (c), but with flattening onto a standardized flat-mounted retina by making four virtual radial cuts \(90^{\circ}\) apart and extending \(3/5\) of meridional length from retinal margin to optic disk. (e,f) Schematic illustration of the mathematical approaches used for the mapping process and transformation between coordinate systems. Parametrization \(\mathbf{x}:\Omega \mapsto \mathbb{R}^3\) of the spherical retina \(S\). Four red meridional arcs show the reconstructed positions of the four radial cuts in the example retina shown in (a) and (c). The cuts have angular coordinates of \(\theta_i\) and an arc length of \(M - m_i\). \(M\) was approximated from the flat-mount as the average lengths of lines running from the optic disk to the retinal margin (green lines, including the folded portions in (a)). \(m_i\) was estimated for each cut by the distance on the flat-mount from optic disk to the terminus of the appropriate radial cut (blue lines in (a), (e) and (f)). Numerical reconstruction of the flat-mounted retina allowed empirical cell locations to be mapped to the spherical retina via the mapping \(\mathbf{x}\circ F^{-1} \).
Outlook:
Using the computational model and through intensive global mapping, we revealed a surprising spherical geometry of retinal DS preferences. We found that ON-, like ON-OFF-DSGCs, comprise four types. Each aligns its DS preference with optic flow produced by translation along one of two axes. These ‘best translational axes’ comprise the gravitational and body axes. They are identical for the two eyes. Thus, each subtype forms a panoramic, binocular ensemble best activated when the animal rises, falls, advances or retreats. These ensembles, while explicitly translational in their geometry, also respond differentially to rotational flow. Any translation or rotation is uniquely encoded by the relative activation of these channels. In particualr we have postulated that the brain can build neurons that prefer translation over rotation, or the reverse, by simple global summation or subtraction of these channels.
References:
Now, it is well known that when animals move, visual and vestibular signals inform the brain which drives postural adjustments, image-stabilizing eye and head movements, and cerebellar learning. It is also well known that otolithic organs (saccule and utricle) encode translation along axes in specific planes, while semicircular canals encode rotation about one of three axes. Geometrically, vestibular planes and axes are orthogonal so that the relative activation of vestibular channels uniquely encodes any possible translation or rotation. On the other hand, when the animal is still moving objects generate "optic flow", the global pattern of retinal image motion. When translating, optic flow diverges from a point in extrapersonal space (the ‘direction of heading’) and converges at a diametrically opposed singularity, see the below image. Features in the animal’s global visual space move along arcs of longitude (meridians) originating from these singularities or poles. When rotating, optic flow circulates around an axis along lines of latitude or, in projection, around a point in visual or retinal space. Rotational and translational optic flow evoke different behaviors, implying divergent encoding mechanisms. Neurons encoding local movement direction are well-known in the eye and brain. Some brain neurons encode global optic flow, but little is known about how these are constructed from retinal inputs and how this relates to the vestibular representation of self-motion. Retinal direction-selective ganglion cells (DSGCs) are neurons on the retina that respond to optic flow aligned in preferred directions. It is believed that DSGCs belong to two classes, the ON and ON-OFF-DSGCs which differ in structure, projections, physiological properties, and functional roles. ON-OFF-DSGCs are further divisible into four subtypes based on preferred direction. They feed retinotopically organized brainstem and cortical centers mediating gaze shifts and conscious motion perception. In contrast, ON DSGCs comprise three subtypes and innervate the accessory optic system (AOS). The AOS encodes rotational optic flow around the best axes of the semicircular canals to mediate image-stabilizing optokinetic reflexes.
In collaboration with biologists David Berson and Shai Sabbah at Brown University I have developed and analyzed a mathematical model of how retinal ganglion cells encode the direction and spatial orientation of perceived objects moving in space. Namely, I developed an elastic model of flat mounted retinas that has been used to relate in-vitro measurements of cell response with in-vivo response of external stimulus. The mathematical model I developed allowed us to understand how the accessory optic system within the brain assembles and compares signals generated by translational and rotational optic flow. The rightmost image below qualitatively compares the measured optic flow with optic flow generated from our models. Namely, the green and red curves are the translational optic flows that are best correlated with our data when mapped to a computational reconstructed retina.

Mathematical model:
My primary role in this project was to develop a mathematical model for reconstructing the retina from measurments of a flat mounted retina. This is essentially like trying to construct an orange from information about the shapes of its peels. Specifically, I modeled the retina as a spherical object \(\mathcal{S}\) of radius \(R\) and maximal longitudinal distance \(M\) with four cuts made along lines of longitude. The retina was parametrized with domain of parametrization \(\mathcal{D}\) by arc length \(s\) as measured from the south pole and \(\theta\) the azimuthal angle. The flattening of the retina was modeled by a mapping \(F:\mathcal{D}\mapsto \mathcal{D}^{\prime} \subset \mathbb{R}^2\) that minimizes an appropriate elastic energy. Specifically, we assumed the retina is an isotropic elastic material with linear stress-strain constitutive relationship and model the per-unit thickness elastic energy of a flattening map \(F\in W^{1,4}(\mathcal{D},\mathcal{D}^{\prime})\) by \[ E[F]=\sum_{i=1}^{4} \int_{\mathcal{D}_i} \left[ \nu\left(\gamma_{11}+\gamma_{22}\right)^2+(1-\nu)\left(\gamma_{11}^2+2\gamma_{12}^2+\gamma_{22}^2\right)\right]\sin\left(\frac{s}{R}\right)ds d\theta,\] where \(\nu\) is the Poisson ratio for the material, \(\gamma_{ij}\) the intrinsic in-plane strain tensor accounting for the curvature of the sphere, and the summation is over each sector of the retina as defined by the cuts. Optimization of this energy was performed using a Rayleigh-Ritz type algorithm. This computational model allowed us to record data from a number of flat mounted retinas and combine it onto a computationally constructed "standard retina".
The diagram below illustrates the various coordinate systems and mapping used to computational reconstruct the retina. (a) Example confocal image of a retina from one experiment. Four radial relieving cuts were made in the eyecup to facilitate flattening, with termini indicated by blue circles. Each magenta vector represents the location and DS preference of a single DSGC. (b) Strain energy density estimating regions of local stretching resulting from the flattening process of the retina. (c-f) Remapping of DSGC locations onto a standardized spherical retinal coordinate system for pooling data across experiments and permitting display in flattened (c,d) or projected spherical form (f). c. Retina in (a) after mapping in standardized spherical coordinates, followed by remapping into flattened form using modeled relieving cuts approximating the actual ones; close similarity to (a) indicates the faithfulness and reversibility of these transformations. (d) Same as (c), but with flattening onto a standardized flat-mounted retina by making four virtual radial cuts \(90^{\circ}\) apart and extending \(3/5\) of meridional length from retinal margin to optic disk. (e,f) Schematic illustration of the mathematical approaches used for the mapping process and transformation between coordinate systems. Parametrization \(\mathbf{x}:\Omega \mapsto \mathbb{R}^3\) of the spherical retina \(S\). Four red meridional arcs show the reconstructed positions of the four radial cuts in the example retina shown in (a) and (c). The cuts have angular coordinates of \(\theta_i\) and an arc length of \(M - m_i\). \(M\) was approximated from the flat-mount as the average lengths of lines running from the optic disk to the retinal margin (green lines, including the folded portions in (a)). \(m_i\) was estimated for each cut by the distance on the flat-mount from optic disk to the terminus of the appropriate radial cut (blue lines in (a), (e) and (f)). Numerical reconstruction of the flat-mounted retina allowed empirical cell locations to be mapped to the spherical retina via the mapping \(\mathbf{x}\circ F^{-1} \).

Outlook:
Using the computational model and through intensive global mapping, we revealed a surprising spherical geometry of retinal DS preferences. We found that ON-, like ON-OFF-DSGCs, comprise four types. Each aligns its DS preference with optic flow produced by translation along one of two axes. These ‘best translational axes’ comprise the gravitational and body axes. They are identical for the two eyes. Thus, each subtype forms a panoramic, binocular ensemble best activated when the animal rises, falls, advances or retreats. These ensembles, while explicitly translational in their geometry, also respond differentially to rotational flow. Any translation or rotation is uniquely encoded by the relative activation of these channels. In particualr we have postulated that the brain can build neurons that prefer translation over rotation, or the reverse, by simple global summation or subtraction of these channels.
References:
- Sabbah, S., Gemmer, J. A., Berson, D., et. al. (2017). A retinal code for motion along the gravitational and body axes. Nature. 546(7659), 492-497.
