PHY 745/785 Group Theory

MWF 12-12:50 PM	OPL 107	http://www.wfu.edu/~natalie/s09phy745/
		http://www.wfu.edu/~ecarlson/groups/

Instructors: Natalie Holzwarth                           Eric Carlson	Phone:758-5510	Office:300 OPL	e-mail:natalie@wfu.edu
	Phone:758-4994	Office:306 OPL	e-mail:ecarlson@wfu.edu

Homework Assignments

Problem Set #1 (1/15/2009)

Problem Set #2 (1/21/2009)

Problem Set #3 (1/23/2009)

Problem Set #4 (1/26/2009)

Problem Set #5 (1/28/2009)

Problem Set #6 (1/30/2009)

Problem Set #7 (2/02/2009)

Problem Set #8 (2/04/2009)

Problem Set #9 (2/06/2009)

Problem Set #10 (2/09/2009)

Problem Set #11 (2/11/2009)

Problem Set #12 (2/13/2009)

Problem Set #13 (2/16/2009)

Problem Set #14 (2/23/2009)

Problem Set #15 (2/25/2009)

Problem Set #16 (2/27/2009)

PHY 745 -- Assignment #1

January 14, 2009

Briefly skim Chapter 1 and read Chapter 2 in Tinkham. This problem has 6 parts and covers material from Lectures 1 & 2. It is due Wed. Jan. 21, 2009.

1. Tinkham Problem #2-1.

January 21, 2009

PHY 745 - Problem Set #2

This homework is due Friday, January 23, 2009.

Continue reading Chapter 3 in Tinkham. For the following matrices $M$, find the similar transformation $S$ which creates the related diagonal matrix $d$:

$$d=S^{-1} M S,$$

choosing $S$ to be unitary whenever appropriate.

1. In this example, $\theta$ represents a real number.
   
   $$M = \left( \begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array} \right).$$
   
   

2. In this example, $\theta$ represents a real number.
   
   $$M = \left( \begin{array}{cc} \cos \theta & \sin \theta \\ \sin \theta & \cos \theta \end{array} \right).$$
   
   

3. In this example, you may wish to ask Maple to help.
   
   $$M = \left( \begin{array}{ccc} 1.0 & 3.0 & 1.0 \\ 0.0 & 2.0 & 0.0 \\ 0.0 & 1.0 & 4.0 \end{array} \right).$$
   
   

PDF version

January 23, 2009

PHY 745 - Problem Set #3

This homework is due Monday, January 26, 2009.

Continue reading Chapter 3 in Tinkham.

1. Consider the following $2 \times 2$ ``normal" matrix $(N N^{\dagger} = N^{\dagger} N)$ in terms of real constants $a$, $b$, $\beta$, and $\gamma$.
   
   $$N = \left( \begin{array}{cc} a & b {\rm {e}}^{i \beta} \\ b {\rm {e}}^{i \gamma} & a \end{array} \right).$$
   
   
   1. Find the eigenvalues $\lambda_i$ and eigenvectors $v_i$
      
      $$N v_i = \lambda_i v_i.$$
      
      

   2. Show that
      
      $$N^{\dagger} v_i = \lambda^*_i v_i.$$
      
      

   3. Find the relationships between the constants for the case that N is Hermitian.
   4. Find the relationships between the constants for the case that N is unitary.

PDF version

January 22, 2009

PHY 745 - Problem Set #4

This homework is due Wednesday, January 28, 2009. You may wish to use Maple to help you with the matrix multiplication. (Please note that Maple's definitions of operators may differ from ours. In particular, Maple's ``Adjoint" is different from ours.)

Continue reading Chapter 3 in Tinkham.

1. On page 8 of Tinkham, you will find an example of 2-dimension representation of the triangular group described by Fig. 2-1 and the multiplication table in the previous page. Consider the following alternative 2-dimension representation:

   
   

   $$E=\left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right),... ...ac{3}{2} \\ -\frac{1}{2} & -\frac{1}{2} \end{array} \right),$$
   
   
   
   
   $$D=\left(\begin{array}{cc} -\frac{1}{2} & -\frac{3}{2} \\ ... ...rac{3}{2} \\ -\frac{1}{2} & -\frac{1}{2} \end{array} \right)$$
   
   
   1. Show that this alternative representation satisfies the group multiplication table.
   2. If the alternative representation is not unitary, use the procedure described in Section 3-2 of your text to transform it into a unitary transformation.

   PDF version
   

   PHY 745 -- Assignment #5

   January 28, 2009

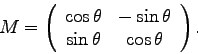
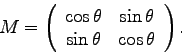
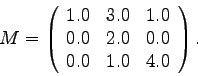
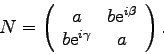
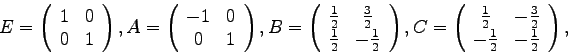
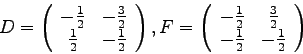
   Continue reading Chapter 3 in Tinkham. This problem is due Fri. Jan. 30, 2009.

   1. Tinkham Problem #3-1. (To save time, you may wish to consult the back of your textbook and verify that the appropriate character table satisfies the necessary relations.)

   PHY 745 -- Assignment #6

   January 30, 2009

   Finish reading Chapter 3 in Tinkham. This problem is due Mon. Feb. 2, 2009.

   1. Find the Character table for a group "i" composed of the identity E and inversion i ( x,y,z -> -x,-y,-z ).
   2. Using the results from HW 5, find the Character table for the direct product group D₄ × i.
   February 2, 2009
   PHY 745 - Problem Set #7
   This homework is due Wednesday, February 4, 2009.

   Finish reading Chapter 3 and start Chapter 4 in Tinkham.

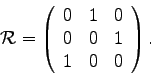   1. Consider the following 3-dimensional transformation matrix
      

      $${\cal{R}} = \left( \begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{array} \right).$$ (1)

      
      
      1. Find Euler angles $\alpha$, $\beta$, and $\gamma$ that correspond to that transformation (with or without inversion).
      2. Consider the transformation of the $l=1$ spherical harmonic functions, using your Euler angles and Eq. 5-36 of your text.
      3. Check that
         

         $$Y_{lm} (\widehat{{\cal{R}} \bf {r}}) = \sum_{m'} Y_{lm'}({\bf {\hat{r}}}) {\cal{D}}^l_{m' m}({\cal{R}}).$$ (2)

         
         

   PDF version
   

   PHY 745 -- Assignment #8

   February 4, 2009

   Start reading Chapter 4 in Tinkham. This problem is due Fri. Feb. 6, 2009.

   A perfect cube has the following 48 symmetry elements designated as transformations on a general point with cartesian coordinates x,y,z with respect the origin at the center of the cube.

   1. x,y,z
   2. -x,y,z
   3. x,-y,z
   4. x,y,-z
   5. -x,-y,z
   6. -x,y,-z
   7. x,-y,-z
   8. -x,-y,-z
   9. y,x,z
   10. -y,x,z
   11. y,-x,z
   12. y,x,-z
   13. -y,-x,z
   14. -y,x,-z
   15. y,-x,-z
   16. -y,-x,-z
   17. x,z,y
   18. -x,z,y
   19. x,-z,y
   20. x,z,-y
   21. -x,-z,y
   22. -x,z,-y
   23. x,-z,-y
   24. -x,-z,-y
   25. z,y,x
   26. -z,y,x
   27. z,-y,x
   28. z,y,-x
   29. -z,-y,x
   30. -z,y,-x
   31. z,-y,-x
   32. -z,-y,-x
   33. y,z,x
   34. -y,z,x
   35. y,-z,x
   36. y,z,-x
   37. -y,-z,x
   38. -y,z,-x
   39. y,-z,-x
   40. -y,-z,-x
   41. z,x,y
   42. -z,x,y
   43. z,-x,y
   44. z,x,-y
   45. -z,-x,y
   46. -z,x,-y
   47. z,-x,-y
   48. -z,-x,-y
   Associate each of these elements with the appropriate class label given in the character table for O_h group on page 329 of your text.

   PHY 745 -- Assignment #9

   February 6, 2009

   Continue reading Chapter 4 in Tinkham. This problem is due Mon. Feb. 9, 2009.

   

   1. The figure shows an object which could have D₃(32) symmetry. If the red and green balls were identical, the object would have D₆(622) symmetry. On page 327 of your text, you will find character tables for the D₆(622) and D₃(32) groups.
      1. Check whether D₃(32) is a subgroup of D₆(622).
      2. Find the compatability relations between the representations of D₃(32) and of D₆(622). (Please define a reasonable notation to distinguish the two group representations.)
   February 8, 2009
   PHY 745 - Problem Set #10
   This homework is due Wednesday, February 11, 2009.

   Continue reading Chapter 4 in Tinkham.

   1. Consider a quantum mechanical free particle of mass $m$ confined within a rectangular box of dimensions $-a \le x \le a$, $-a \le y \le a$, and $-b \le z \le b$.
      1. Check that the eigenstates of the particle all vanish on the 6 planes that bound the box and take the form:
         
         $$\Psi_{lmn}(x,y,z) = \frac{1}{\sqrt{a^2b}} \; w_l\left( \fra... ...{m \pi y}{2a}\right) \; w_n\left( \frac{n \pi y}{2b}\right),$$
         
         
         where
         
         $$w_n(u) = \left\{ \begin{array}{ll} \cos(u) & {\mbox{\rm {if... ...rm {if }}} n \equiv {\mbox{\rm { even}}} \end{array} \right.$$
         
         

      2. Now consider these states with reference to the $D_4$ point group discussed in your text book and in the Notes for Lecture 9 - http://www.wfu.edu/~natalie/s09phy745/lecturenote/ . From the character table for this point group, for each irreducible representation, find at least one example of a basis function from the $\Psi_{lmn}(x,y,z)$ eigenstates.
   PDF version

   PHY 745 -- Assignment #11

   February 11, 2009

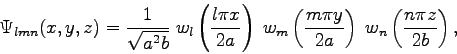
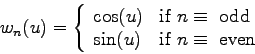
   Continue reading Chapter 4 in Tinkham. This problem is due Fri. Feb. 13, 2009.

   1. An Nd⁺² ion in its ground state in a spherical environment has total orbital angular momentum L=6. Suppose that this ion is introduced into a crystal at a site that has O_h symmetry. What are the compabible irreducible representations of the ion?

                                                      Physics 745 - Group Theory

                                                      Homework Set 12    Due Monday, February  16

   Note: the lecture and homework set was prepared by Prof. Carlson.

    

   1.  Diamond is a version of carbon. The position of the carbon atoms takes the form

   

         where d = 356.683 pm,  are arbitrary integers, and  takes on the following eight values:

   

         Thus there are eight carbon atoms per cell of size d³.

   (a) For what values of  will  be a translation vector; i.e., if there is a carbon atom at r, there will always be a carbon atom at ?  To make your answer finite, only include values with .

   (b)  Find primitive vectors a, b and c such that all translation vectors take the form , where  are integers.  Demonstrate it explicitly for those vectors you found in part (a) (which will probably be trivial), and also for the three vectors ,  and .

   (c)  What are the lengths of these vectors  and the angles between them, ?

    

   PDF version

   PHY 745 -- Assignment #13

   February 16, 2009

   Continue reading Chapter 4 in Tinkham. This problem is due Wed. Feb. 18, 2009.

   1. Consider a monoclinic lattice in the "first setting" with non-orthogonal angle γ. The conventional translation vectors are given by
      a = a x
      b = b ( cos γ x + sin γ y)
      c = c z
      and the lattice positions are
      τ₁ = 0
      τ₂ = ½ a + ½ c.
      
      1. Show that the same lattice can be generated using the primitive lattice translations
         T₁ = ½ a + ½ c
         T₂ = b
         T₃ = ½ a - ½ c
         
      2. What are the volumes of the conventional and primitive unit cells?

   PHY 745 -- Assignment #14

   February 23, 2009

   Continue reading Chapters 4 and 8 in Tinkham. This problem is due Wed. Feb. 25, 2009.

   Consider the following two examples of crystals which have the fcc (O_h⁵) structure. For each, find an expression for their structure factors S(Δk). For evaluating the atomic structure factors, you may use the expression

   F_a(Δk) = Z_a exp(-|Δk|² &Lambda_a²/4), where the index "a" and the related parameters will depend on the kind of atom. For both crystals, the primitive lattice and reciprocal lattice vectors are given by

   Real space lattice	Reciprocal space lattica
   T1=(a/2)*(x+y)	G1=(2π/a)*(x+y-z)
   T2=(a/2)*(x+z)	G2=(2π/a)*(x-y+z)
   T3=(a/2)*(y+z)	G3=(2π/a)*(-x+y+z)

   1. Consider the NaCl lattice where within the reference cell a Na is located at σ_Na=0 and a Cl is located at σ_Cl=(a/2)*(x+y+z).
   2. Consider the diamond lattice where within the reference cell one C is located at σ_C1=(a/8)*(x+y+z) and the other is located at σ_C2=-(a/8)*(x+y+z).

   PHY 745 -- Assignment #15

   February 25, 2009

   Continue reading Chapters 4 and 8 in Tinkham. This problem is due Fri. Feb. 27, 2009.

   

   1. Consider the above diagram of the Brillouin Zone of a cube taken from the paper of Bouckaert, Smoluchowski, and Wigner (Phys. Rev. 50, 58 (1936) The Γ point has the point group symmetry ({R|0}) of cubic space group -- ({R|t}) -- O_h.
      1. For at least 3 lines within the Brillouin Zone (such as Σ, Δ, &Lambda) find the point group symmetries which describe Bloch states of the crystal with those wave vectors.
      2. For at least 3 points within the Brillouin Zone (such as X, M, R) find the point group symmetries which describe Bloch states of the crystal with those wave vectors.

   PHY 745 -- Assignment #16

   February 27, 2009

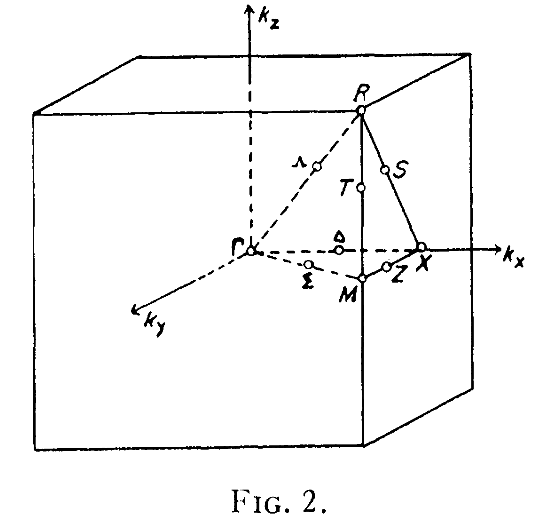
   Continue reading Chapters 4 and 8 in Tinkham. This problem is due Mon. Mar. 2, 2009.

   1. Consider a molecule C₃ which takes the form of an equilateral triangle. (I am not sure such a molecule is stable...) In equilibrium this molecule has D_3h symmetry. Since there are 3 atoms, there are 3 × 3 = 9 normal modes of vibration, 3 of which have non-zero frequency. (The other 6 modes involve uniform translation or rotation.)
      1. Using the D_3h character table on page 328 of your text, find the number of times each irreducible representation characterizes a general vibrational mode.
      2. Determine which of these irreducible representations correspond to the non-trivial (non zero-frequency) modes.
   [an error occurred while processing this directive] Last modfied: Friday, 27-Feb-2009 09:07:25 EST