| General Chemistry | ||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
| Organic Chemistry | ||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
| General Physics | ||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
| General Math | ||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
General Physics :: Projectile Motion :: Introduction
What is projectile motion?
Projectile motion refers to a particular form of 2-dimensional motion.
Examples: the motion of a baseball (or any object) thrown into the
air, or, as in the cannon ball projectile game found on this web
site, a waterballoon shot from a cannon.
Problem to Solve in Playing the Cannon Ball Projectile Game:
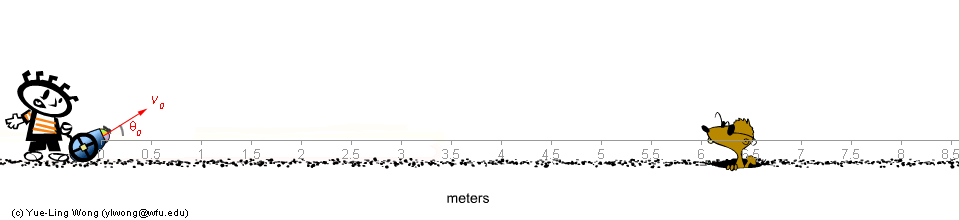 Figure 1.
Figure 1.
Given the initial velocity of the cannon ball, v0, and its angle of firing, θ0 (Figure 1 above), can you predict:
- Problem #1: where the cannon ball will land? (horizontal motion analysis; cannon ball game level 2) (See section How to Calculate #1)
- Problem #2: the maximum height the cannon ball can go? (vertical motion analysis)
- Problem #3: what is the cannon ball's horizontal location when it reaches the highest point? (both horizontal and vertical motion analyses; cannon ball game level 3)
For examples:
if v0 = 8 m/second and θ0 = 30o, the waterballoon will take about 0.8 second to land at about 5.7 m from the cannon.
if v0 = 4 m/second and θ0 = 30o, the waterballoon will take about 0.4 second to land at about 1.4 m from the cannon.
if v0 = 8 m/second and θ0 = 45 o, the waterballoon will take about 1.2 second to land at about 6.5 m from the cannon.
Based on the three examples above, you see:
- If the firing angle is kept the same, doubling the initial velocity will increase the landing distance 4 times.
- If the initial velocity is kept the same, increasing the firing angle will increase the time it takes for the waterballoon to land.
In the sections of How to Calculate #1 - #3, you will see a step-by-step calculation to solve the Problems #1 - #3, respectively.
After you have learned how to determine where the cannon ball will land, you can then perform several calculation to use a guide to play the Cannon Ball (waterballoon) Soak-A-Mole Game.
In the interactive Cannon Ball Projectile below, experiment and observe how (1) the initial velocity of the cannon ball, v0, and (2) its angle of firing, θ0, affect:
(a) the landing distance of the water balloon;
(b) the maximum height of the water balloon's parabolic motion path.
How to play:
- Click once in the game below to start
- UP / DOWN arrow keys: adjust the angle of firing
- LEFT / RIGHT arrow keys: move the kid and the cannon
- SPACEBAR:
- hold down the spacebar to increase velocity
- release the spacebar to fire
- Drag the ruler to any location if you want to do measurements.
Note: The above game does not have the mole; it is just a water balloon shooting practice. The background color of the game changes according to your computer's time. Depending on what time you are playing, you may even see "virtual" sunrise or sunset while you are shooting water balloons!
[an error occurred while processing this directive]