GREY BALLARD

About Research Publications Textbook Software Teaching

High Performance Tensor Computations

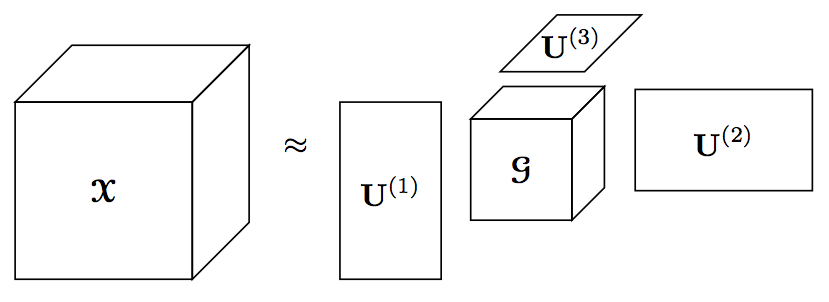
(Tucker model)

Advances in sensors and measurement technologies, extreme-scale scientific simulations, and growing digital communications all contribute to a data avalanche that is overwhelming analysts. Standard data analytic techniques often require information to be organized into two-dimensional tables, where, for example, rows correspond to subjects and columns correspond to features. However, many of today's data sets involve multi-way relationships and are more naturally represented in higher-dimensional tables called tensors. For example, movies are naturally 3D tensors, communication information tracked between senders and receivers across time and across multiple modalities can be represented by a 4D tensor, and scientific simulations tracking multiple variables in three physical dimensions and across time are 5D tensors. Tensor decompositions are the most common method of unsupervised exploration and analysis of multidimensional data. These decompositions can be used to discover hidden patterns in data, find anomalies in behavior, remove noise from measurements, or compress prohibitively large data sets. The aim of this project is to develop efficient algorithms for computing these decompositions, allowing for analysis of multidimensional datasets that would otherwise take too much time or memory.

This research is aligned with the Sparsitute, a Mathematical Multifaceted Integrated Capability Center (MMICC) funded by the US Department of Energy. Sparsitute brings together leading researchers across the nation working on various aspects of sparsity to accelerate progress and impact. Our ambitious research agenda will drastically advance the state-of-the-art in sparse computations both as a unified topic and within three broad pillars: sparse and structured matrix computations, sparse tensor problems, and sparse network problems, as well as their interconnections.

Relevant Papers/Talks

Robust, Scalable, and Practical Low-Rank Approximation
for Scalable Data Analytics

(Hyperspectral image tree)

Matrix and tensor low rank approximations have been foundational tools in numerous science and engineering applications. By imposing constraints on the low rank approximations, we can model many key problems and design scalable algorithms for Big Data analytics that reach far beyond the classical science and engineering disciplines. In particular, mathematical models with nonnegative data values abound across application fields, and imposing nonnegative constraints on the low rank models make the discovered latent components interpretable and practically useful. Variants of these constraints can be designed to reflect additional characteristics of real-life data analytics problems.

The goals of this research are (1) to develop efficient parallel algorithms for computing nonnegative matrix and tensor factorizations (NMF and NTF) and their variants using a unified framework, and (2) to produce a software package that delivers the high performance, flexibility, and scalability necessary to tackle the ever-growing size of today’s data sets.

Relevant Papers/Talks

Communication-Avoiding Algorithms

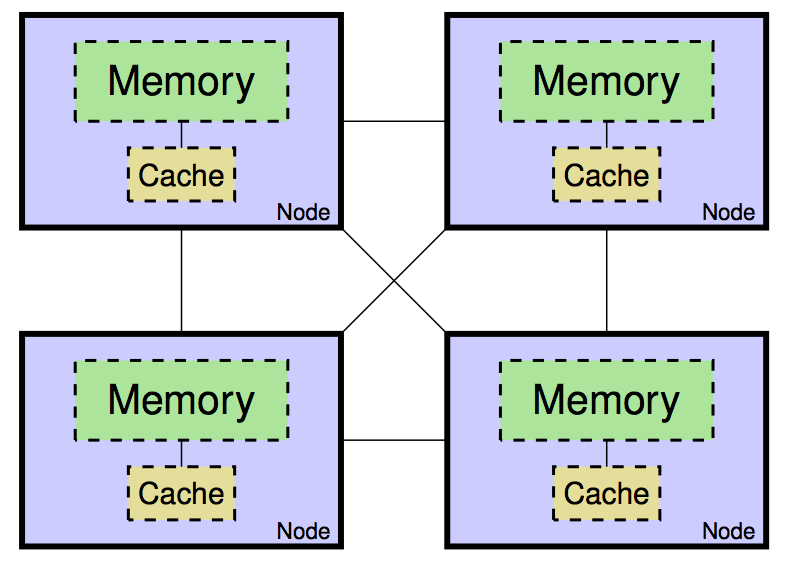
(Parallel machine model)

The traditional metric for the efficiency of an algorithm has been the number of arithmetic operations it performs. Technological trends have long been reducing the time to perform an arithmetic operation, so it is no longer the bottleneck in many algorithms; rather, communication, or moving data, is the bottleneck. This motivates us to seek algorithms that move as little data as possible, either between levels of a memory hierarchy or among parallel processors over a network.

The idea of communication-avoiding algorithms is to reformulate existing approaches to solving fundamental problems in order to significantly reduce the amount of data movement. Using abstract machine models, we strive to prove communication lower bounds, determining the minimum amount of data movement any algorithm must perform. Then we can compare the communication costs of existing approaches to the lower bounds to determine if algorithmic improvements are possible. If there exists a gap between best algorithm and best known lower bound, the goal becomes to close the gap, usually with an innovative algorithm. In this case, the ultimate goal is to implement the algorithm on state-of-the-art hardware to achieve practical performance improvements for today’s applications.

Relevant Papers/Talks

Practical Fast Matrix Multiplication

(Tucker model)
(Tucker model)

Strassen surprised the field of computer science in 1969 with a simple recursive algorithm for dense matrix multiplication that requires asymptotically fewer arithmetic operations than the traditional approach. For multiplying two square matrices of dimension n, his algorithm requires O(n2.81) operations, while the traditional dot-product based algorithm requires O(n3). His discovery sparked decades of research into “fast” matrix multiplication algorithms in the fields of pure mathematics, theoretical computer science, and high performance computing that continues today. There exists a theoretical goal of discovering ω, the true exponent of matrix multiplication, and at the same time, there exists a practical goal of leveraging fast algorithms to benefit the many applications that rely on dense matrix multiplication as a computational kernel.

The goal of this project is to connect the theoretical and practical research on the topic to discover and implement practical fast algorithms so that they can benefit applications. Strassen’s original algorithm has been demonstrated to decrease run times of matrix multiplications of reasonable sizes, even compared against heavily tuned library implementations of the classical algorithm. Recently, a wealth of new algorithms have been discovered, and there is renewed interest both in demonstrating that these algorithms are also practical and in using computer-aided search to discover new algorithms. While this problem is one of the most intensely studied in computer science, modern computational capabilities are opening up new possibilities for research breakthroughs.

Relevant Papers/Talks

Visualizing Parallel Algorithms

(Parallel Knapsack)
(Parallel Mergesort)

The design and analysis of parallel algorithms are both fundamental to the set of high-performance, parallel, and distributed computing skills required to use modern computing resources efficiently. In this project, we present an approach of teaching parallel computing within an undergraduate algorithms course that combines the paradigms of divide-and-conquer algorithms and dynamic programming along with multithreaded parallelization. Using the Thread Safe Graphics Library, we have developed a set of visualization tools that enables interactive demonstration of parallelization techniques for two fundamental dynamic programming problems, 0/1 Knapsack and Longest Common Subsequence, and Mergesort. The tools are publicly available to be used directly or as a basis on which to build visualizations of similar algorithms.

Relevant Papers/Talks