Self Similar Growth Patterns
The rippling patterns observed in swelling hydrogels, leaves, and torn plastic provide striking examples of periodic and self-similar patterns; see the figure below. While numerical experiments set within the framework of finite elasticity have been able to qualitatively replicate these patterns, they do not provide a complete mathematical understanding of the mechanism behind the self-similar patterns. Generically, such complex, self similar patterns are usually associated with "strongly frustrated" systems, e.g. elastic sheets with boundary conditions that preclude the possibility of relieving in plane strains, or at alloy-alloy interfaces between distinct crystal structures. In my work I seek to understand how such complex geometries are selected by minimization of elastic energy.

Mathematical model:
One model of growing thin elastic sheets is the non-Euclidean model of elasticity which posits that growth permanently deforms the intrinsic distance between material points. Material points on the center surface are labelled by material coordinates \((x,y) \in \Omega\subset \mathbb{R}^2\), and the natural distances between points in the center surface are encoded in the arc length element: \[ ds^2=g_{11}(x,y)dx^2+2g_{12}(x,y)dxdy+g_{22}(x,y)dy^2, \] with \(g_{ij}\) the components of a Riemannian metric \(\mathbf{g}\). That is, the Riemannian metric \(\mathbf{g}\) models the growth process by encoding the distorted strain free distance between material coordinates. By the Kirchoff hypothesis, the conformation of the sheet as a 3-dimensional object in \(\mathbb{R}^3\) is determined by an immersion \(F:\Omega \to \mathbb{R}^3\) of the center surface. By Gauss's Theorema Egregium, \(\mathbf{g}\) generates an intrinsic definition of Gaussian curvature \(K\) throughout the sheet. Locally \(K<0\) \((K>0)\) correspond to the regions in which local growth (atrophy) occur in the sheet. In this framework, the elastic energy is then modeled as the sum of stretching and bending contributions: \[ E[F]=\mathcal{S}[\nabla F]+t^2\mathcal{B}[D^2F]=\int_{\Omega} \|(\nabla F )^T \cdot \nabla F-\mathbf{g}\|^2\,dxdy+t^2 \int_{\Omega}\left(k_1^2+k_2^2\right)\,dxdy, \] where \(t\) is the thickness of the sheet, \(D^2F\) denotes the Hessian of \(F\), and \(k_1,k_2\) are the principal curvatures of \(F\).
Due to the relative strength of stretching to bending rigidity it is natural to expect that thin sheets deform into low bending energy configurations that remove all in-plane strain. This corresponds to the ``restricted'' problem of minimizing the bending energy over all isometric immersions of the Riemannian 2-manifold \((\Omega,\mathbf{g})\), i.e. deformations satisfying \((\nabla F)^T\cdot \nabla F=\mathbf{g}\). Indeed, provided they exist, finite bending energy isometric immersions of \((\Omega,\mathbf{g})\) are the \(t \to 0\) limits of minimizers of the ``full" elastic energy. For \(K\) uniformly negative, however, the extrinsic geometry of the system imposes that with increasing domain size smooth isometries will develop singularities where one of the principal curvatures diverges and for \(K=-1\) these singularities form curves - "singular edges" - across which the bending energy diverges. Moreover, the Nash embedding Theorem guarantees the existence of at least \(C^1\) regular isometric immersions but these surfaces are too rough to be candidates for a minimizer. A natural question then is what are the behavior of minimizers of the elastic energy given the constraints on the regularity of isometric immersions for hyperbolic metrics.
Isometries and bending energy:
In reference [1] we investigated finite bending energy isometric immersions of the strip \(\Omega=\mathbb{R} \times [0,W]\) with the metric \[ \mathbf{g}=(1+2 \epsilon^2 f(y))\,dx^2+dy^2, \quad f(y) = \frac{\alpha}{4 (\alpha+1)} \left(1+\frac{y}{l}\right)^{-\alpha} \] where \(\alpha\in (0,\infty)\), \(l\) is a length scale and \(\epsilon>0\). These metrics corresponds to \(y\) dependent growth in the \(x\) direction localized near the \(y=0\) edge of the sheet. It includes the metrics considered in prior numerical studies as particular cases.
For \(\epsilon \ll1 \), approximate isometries are obtained from the Foppl - von Karman ansatz \(F(x,y) = (x+\epsilon^2 u,y+\epsilon^2v,\epsilon w)\) with \(O(\epsilon^2)\) in-plane and \(O(\epsilon)\) out-of-plane deformations. In the small slope regime, i.e. for \(\epsilon \ll 1\), the mean and Gaussian curvatures are given by \(H=\frac{\epsilon}{2}\Delta w\) and \(K=\epsilon^2 \det(D^2 w)\). If \(w\) satisfies \[ \det(D^2 w(x,y))= w_{xx}w_{yy} - (w_{xy})^2 = -f^{\prime \prime} = -\frac{\alpha^2}{4}\left(1+\frac{y}{l}\right)^{-\alpha-2}, \] the small-slope version of Gauss' Theorema Egregium, we can solve for the in-plane displacements \(u\) and \(v\) to obtain isometries at \(O(\epsilon^2)\). This equation has a one parameter family of product solutions \[w^0(x,y) = k^{-1} \psi(k x) \left(1+y/l\right)^{-\alpha/2} \] where \(\psi'^2 + |\psi|^{2\alpha/(2+\alpha)} = 1\). These product solutions for \(w\) necessarily yield single wavelength isometries. The wavelength in the \(x\) direction is set by \(k\) and is independent of \(y\) so there is no refinement as \(y \to 0\). For the product solution, the mean curvature is given by \[ H(x,y) =\epsilon \left[\frac{c_1(\xi) }{kl^2(1+y/l)^{\alpha/2+2}} - \frac{c_2(\xi) k}{ (1+y/l)^{\alpha/2}}\right], \] where \(\xi = k x\), and \(c_{1,2}\) are positive functions, independent of \(k\).
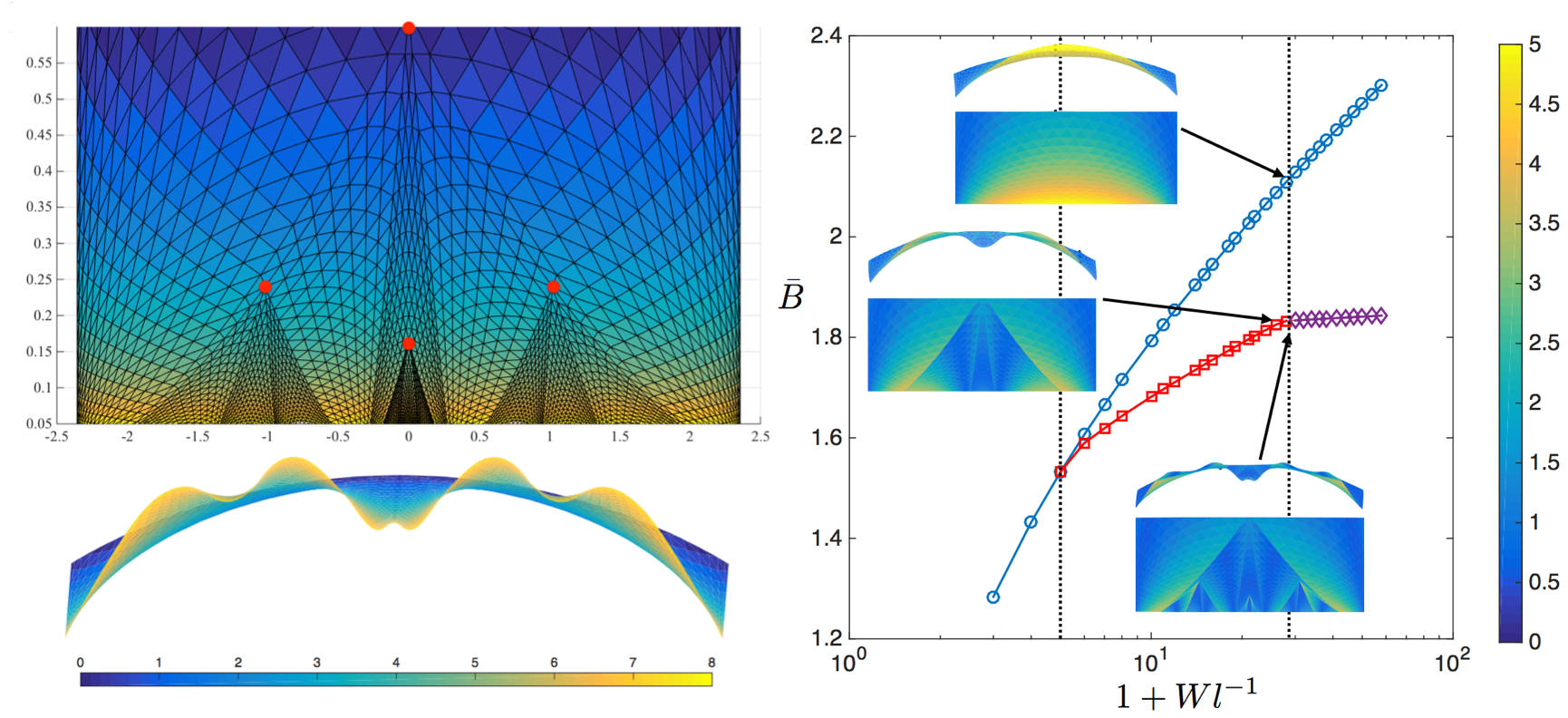
The mean curvature quantifies the local disparity between the energetic contributions of different wavelengths throughout the sheet. Averaging \(\epsilon^{-2}H^2\) over a quarter-period \(\lambda_k\) and optimizing over \(k\) the optimal "global" wavelength" \(\lambda_{glob}\) is given by: \[ \lambda_{glob} \sim \frac{1}{k^*} \sim l \left|\frac{ \left(1+W/l\right)^{1-\alpha}-1}{\left(1+W/l\right)^{-3-\alpha}-1} \right|^{\frac{1}{4}} , \] where we are taking \(|(1+W/l)^{1-\alpha}-1|=\ln\left(1+W/l\right)\) for \(\alpha=1\). We can also determine the optimal "local" wavelength \(\lambda_{loc}(y)\) by minimizing the average of \(H^2\) at a given \(y\), without integrating in \(y\) to obtain \[ \lambda_{loc}(y) \sim l (1+y/l) = (y+l). \] For \(W \gg l\), there is a range of \(y\) where \(\lambda_{loc}(y)\) differs substantially from \(\lambda_{glob}\), giving an energetic impetus for the sheet to increase the buckling wavelength as one moves away from the edge at \(y=0\).
Branch points:
There are geometrical restrictions that restrict smooth is constant and negative (link to this study) within the "small slope" approximation. In this work we showed that to break the rigid single wavelength constraint it is necessary to introduce what we have called "branch points" into the isometry.
To see how this construction works, first consider solutions of line of inflection -- a principal curvature for the surface \(z=w(x,y)\) is discontinuous across this ray, but the bending energy density is finite. Now, the key point is that a quadratic sufrace is entirely ruled by straight asymptotic lines and thus this construction can be extended to any point \((x_0,y_0)\) on the quadratic surface; see the below figure. Namely, by appropriately joining versions \(w(x,y)\) of solutions to the Monge-Ampre equation along these lines of infection we can generalize our construction to different points on the surface. The resulting surface is not smooth but has finite bending energy i.e. it has \(W^{2,2}\) regularity.
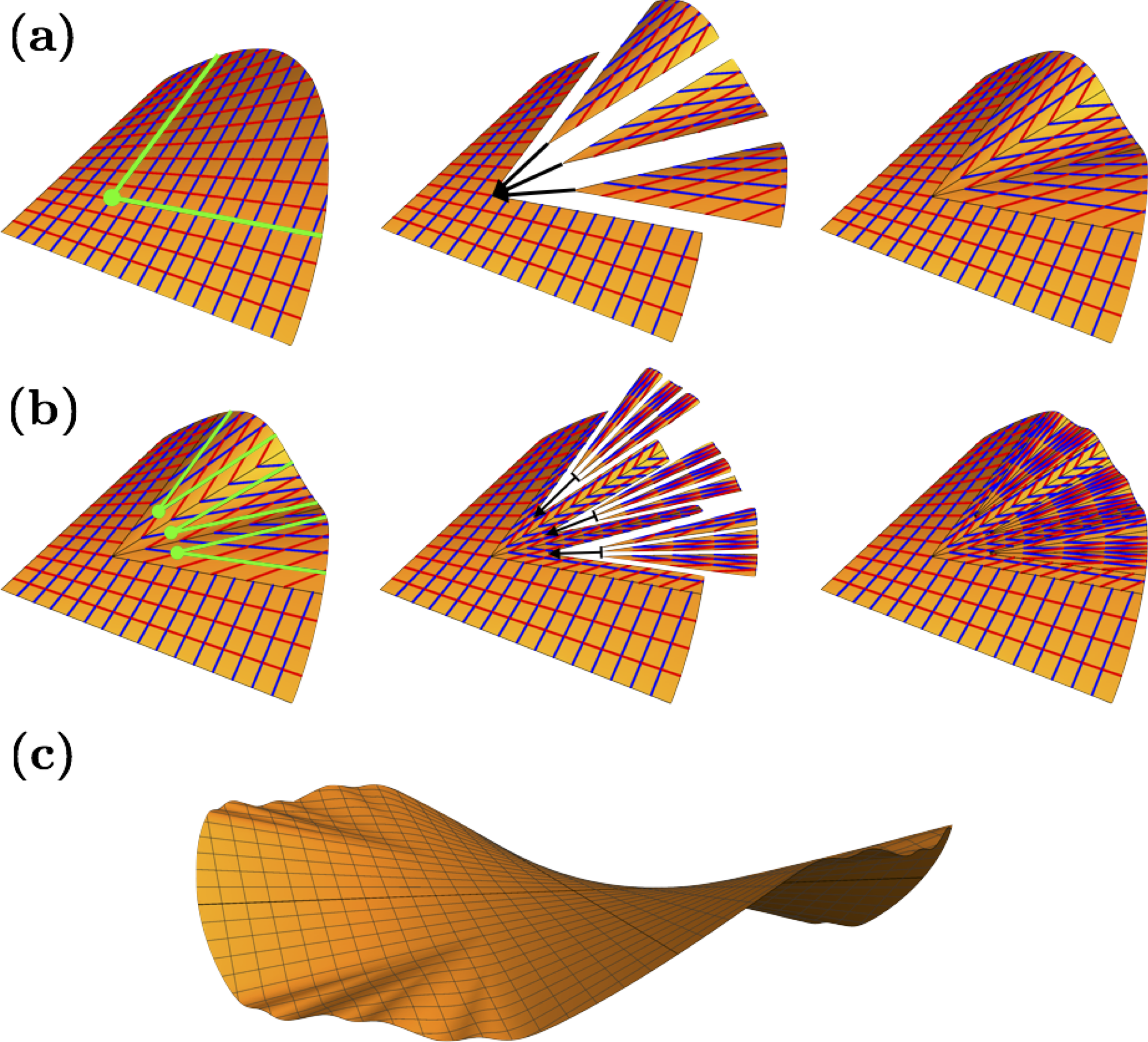
Self similar patterns:
Returning to the strip geometry, we want to create patterns which have an effective wavelength that increases with \(y\), so they have lower energy than the single wavelength isometry. A natural idea is to introduce branch points into the product solutions to allow for local refinement of the wavelength near \(y=0\). However, the product solutions are not ruled by straight lines, and it is not immediately obvious how one adapts the above construction. However, the key concept in our above construction was not that we were introducing "lines of inflection" along straight lines but rather asymptotic curves on the surface, that is curves along which the normal curvature vanishes. Indeed, the Beltrami-Enneper theorem states that the torsion of an asymptotic curve is proportional to the Gaussian curvature. Hence, when gluing isometries along asymptotic curves when can preserve the rotation of the surface normal, i.e. we can guarantee \(W^{2,2}\) regularity.
In reference [4] we used a discretization of the strip geometry along asymptotic curves to introduce branch points onto the surface. The benefit of this approach was that it allowed for easy implementation of boundary conditions. The below figure illustrates a "discrete isometric immersion" obtained by introducing branch points into the above product solutions. As the step size of the discretization goes to zero, the asymptotic net converges, by construction, to a surface with a continuously varying tangent plane, i.e. no ridges or cone-points. As we conjectured above, the introduction of branch points allowing for local of refinement of the patterns does lower the bending content in the sheet. Thus, branch points are the natural geometric mechanism that allows for the self-similar patterns observed in swelling thin elastic sheets.
Outlook:
The existence of small-slope isometric immersions for hyperbolic free sheets with finite bending content ensures that the elastic energy per unit thickness scales as \(t^2\). Free sheets therefore do not admit elastic ridges, \(d\)-cones or wrinkles that balance stretching and bending energies because these defects cost too much energy; rather, the relevant singularities are branch points and lines of inflection. These defects are unique in that they do not concentrate elastic energy in the vanishing thickness limit. They arise as a mechanism to bypass the rigidity of smooth isometric immersions that prevents the refinement of the pattern wavelength. To our knowledge, this is the first example of a condensed matter system that is driven by geometric rather than energetic defects.
Our construction shows there are continuous families of low-energy states obtained by appropriately gluing together isometries. Variations within these families lead to "floppy modes" of deformation. Thin hyperbolic free sheets are thus easily deformed by weak stresses. The buckling pattern may be sensitive to the dynamics of the swelling process, experimental imperfections, or other external forces. A statistical description of the singularities and their interactions is therefore a natural approach to study this system.
References:

Mathematical model:
One model of growing thin elastic sheets is the non-Euclidean model of elasticity which posits that growth permanently deforms the intrinsic distance between material points. Material points on the center surface are labelled by material coordinates \((x,y) \in \Omega\subset \mathbb{R}^2\), and the natural distances between points in the center surface are encoded in the arc length element: \[ ds^2=g_{11}(x,y)dx^2+2g_{12}(x,y)dxdy+g_{22}(x,y)dy^2, \] with \(g_{ij}\) the components of a Riemannian metric \(\mathbf{g}\). That is, the Riemannian metric \(\mathbf{g}\) models the growth process by encoding the distorted strain free distance between material coordinates. By the Kirchoff hypothesis, the conformation of the sheet as a 3-dimensional object in \(\mathbb{R}^3\) is determined by an immersion \(F:\Omega \to \mathbb{R}^3\) of the center surface. By Gauss's Theorema Egregium, \(\mathbf{g}\) generates an intrinsic definition of Gaussian curvature \(K\) throughout the sheet. Locally \(K<0\) \((K>0)\) correspond to the regions in which local growth (atrophy) occur in the sheet. In this framework, the elastic energy is then modeled as the sum of stretching and bending contributions: \[ E[F]=\mathcal{S}[\nabla F]+t^2\mathcal{B}[D^2F]=\int_{\Omega} \|(\nabla F )^T \cdot \nabla F-\mathbf{g}\|^2\,dxdy+t^2 \int_{\Omega}\left(k_1^2+k_2^2\right)\,dxdy, \] where \(t\) is the thickness of the sheet, \(D^2F\) denotes the Hessian of \(F\), and \(k_1,k_2\) are the principal curvatures of \(F\).
Due to the relative strength of stretching to bending rigidity it is natural to expect that thin sheets deform into low bending energy configurations that remove all in-plane strain. This corresponds to the ``restricted'' problem of minimizing the bending energy over all isometric immersions of the Riemannian 2-manifold \((\Omega,\mathbf{g})\), i.e. deformations satisfying \((\nabla F)^T\cdot \nabla F=\mathbf{g}\). Indeed, provided they exist, finite bending energy isometric immersions of \((\Omega,\mathbf{g})\) are the \(t \to 0\) limits of minimizers of the ``full" elastic energy. For \(K\) uniformly negative, however, the extrinsic geometry of the system imposes that with increasing domain size smooth isometries will develop singularities where one of the principal curvatures diverges and for \(K=-1\) these singularities form curves - "singular edges" - across which the bending energy diverges. Moreover, the Nash embedding Theorem guarantees the existence of at least \(C^1\) regular isometric immersions but these surfaces are too rough to be candidates for a minimizer. A natural question then is what are the behavior of minimizers of the elastic energy given the constraints on the regularity of isometric immersions for hyperbolic metrics.
Isometries and bending energy:
In reference [1] we investigated finite bending energy isometric immersions of the strip \(\Omega=\mathbb{R} \times [0,W]\) with the metric \[ \mathbf{g}=(1+2 \epsilon^2 f(y))\,dx^2+dy^2, \quad f(y) = \frac{\alpha}{4 (\alpha+1)} \left(1+\frac{y}{l}\right)^{-\alpha} \] where \(\alpha\in (0,\infty)\), \(l\) is a length scale and \(\epsilon>0\). These metrics corresponds to \(y\) dependent growth in the \(x\) direction localized near the \(y=0\) edge of the sheet. It includes the metrics considered in prior numerical studies as particular cases.
For \(\epsilon \ll1 \), approximate isometries are obtained from the Foppl - von Karman ansatz \(F(x,y) = (x+\epsilon^2 u,y+\epsilon^2v,\epsilon w)\) with \(O(\epsilon^2)\) in-plane and \(O(\epsilon)\) out-of-plane deformations. In the small slope regime, i.e. for \(\epsilon \ll 1\), the mean and Gaussian curvatures are given by \(H=\frac{\epsilon}{2}\Delta w\) and \(K=\epsilon^2 \det(D^2 w)\). If \(w\) satisfies \[ \det(D^2 w(x,y))= w_{xx}w_{yy} - (w_{xy})^2 = -f^{\prime \prime} = -\frac{\alpha^2}{4}\left(1+\frac{y}{l}\right)^{-\alpha-2}, \] the small-slope version of Gauss' Theorema Egregium, we can solve for the in-plane displacements \(u\) and \(v\) to obtain isometries at \(O(\epsilon^2)\). This equation has a one parameter family of product solutions \[w^0(x,y) = k^{-1} \psi(k x) \left(1+y/l\right)^{-\alpha/2} \] where \(\psi'^2 + |\psi|^{2\alpha/(2+\alpha)} = 1\). These product solutions for \(w\) necessarily yield single wavelength isometries. The wavelength in the \(x\) direction is set by \(k\) and is independent of \(y\) so there is no refinement as \(y \to 0\). For the product solution, the mean curvature is given by \[ H(x,y) =\epsilon \left[\frac{c_1(\xi) }{kl^2(1+y/l)^{\alpha/2+2}} - \frac{c_2(\xi) k}{ (1+y/l)^{\alpha/2}}\right], \] where \(\xi = k x\), and \(c_{1,2}\) are positive functions, independent of \(k\).
The mean curvature quantifies the local disparity between the energetic contributions of different wavelengths throughout the sheet. Averaging \(\epsilon^{-2}H^2\) over a quarter-period \(\lambda_k\) and optimizing over \(k\) the optimal "global" wavelength" \(\lambda_{glob}\) is given by: \[ \lambda_{glob} \sim \frac{1}{k^*} \sim l \left|\frac{ \left(1+W/l\right)^{1-\alpha}-1}{\left(1+W/l\right)^{-3-\alpha}-1} \right|^{\frac{1}{4}} , \] where we are taking \(|(1+W/l)^{1-\alpha}-1|=\ln\left(1+W/l\right)\) for \(\alpha=1\). We can also determine the optimal "local" wavelength \(\lambda_{loc}(y)\) by minimizing the average of \(H^2\) at a given \(y\), without integrating in \(y\) to obtain \[ \lambda_{loc}(y) \sim l (1+y/l) = (y+l). \] For \(W \gg l\), there is a range of \(y\) where \(\lambda_{loc}(y)\) differs substantially from \(\lambda_{glob}\), giving an energetic impetus for the sheet to increase the buckling wavelength as one moves away from the edge at \(y=0\).
Branch points:
There are geometrical restrictions that restrict smooth is constant and negative (link to this study) within the "small slope" approximation. In this work we showed that to break the rigid single wavelength constraint it is necessary to introduce what we have called "branch points" into the isometry.
To see how this construction works, first consider solutions of line of inflection -- a principal curvature for the surface \(z=w(x,y)\) is discontinuous across this ray, but the bending energy density is finite. Now, the key point is that a quadratic sufrace is entirely ruled by straight asymptotic lines and thus this construction can be extended to any point \((x_0,y_0)\) on the quadratic surface; see the below figure. Namely, by appropriately joining versions \(w(x,y)\) of solutions to the Monge-Ampre equation along these lines of infection we can generalize our construction to different points on the surface. The resulting surface is not smooth but has finite bending energy i.e. it has \(W^{2,2}\) regularity.

Self similar patterns:
Returning to the strip geometry, we want to create patterns which have an effective wavelength that increases with \(y\), so they have lower energy than the single wavelength isometry. A natural idea is to introduce branch points into the product solutions to allow for local refinement of the wavelength near \(y=0\). However, the product solutions are not ruled by straight lines, and it is not immediately obvious how one adapts the above construction. However, the key concept in our above construction was not that we were introducing "lines of inflection" along straight lines but rather asymptotic curves on the surface, that is curves along which the normal curvature vanishes. Indeed, the Beltrami-Enneper theorem states that the torsion of an asymptotic curve is proportional to the Gaussian curvature. Hence, when gluing isometries along asymptotic curves when can preserve the rotation of the surface normal, i.e. we can guarantee \(W^{2,2}\) regularity.
In reference [4] we used a discretization of the strip geometry along asymptotic curves to introduce branch points onto the surface. The benefit of this approach was that it allowed for easy implementation of boundary conditions. The below figure illustrates a "discrete isometric immersion" obtained by introducing branch points into the above product solutions. As the step size of the discretization goes to zero, the asymptotic net converges, by construction, to a surface with a continuously varying tangent plane, i.e. no ridges or cone-points. As we conjectured above, the introduction of branch points allowing for local of refinement of the patterns does lower the bending content in the sheet. Thus, branch points are the natural geometric mechanism that allows for the self-similar patterns observed in swelling thin elastic sheets.

Outlook:
The existence of small-slope isometric immersions for hyperbolic free sheets with finite bending content ensures that the elastic energy per unit thickness scales as \(t^2\). Free sheets therefore do not admit elastic ridges, \(d\)-cones or wrinkles that balance stretching and bending energies because these defects cost too much energy; rather, the relevant singularities are branch points and lines of inflection. These defects are unique in that they do not concentrate elastic energy in the vanishing thickness limit. They arise as a mechanism to bypass the rigidity of smooth isometric immersions that prevents the refinement of the pattern wavelength. To our knowledge, this is the first example of a condensed matter system that is driven by geometric rather than energetic defects.
Our construction shows there are continuous families of low-energy states obtained by appropriately gluing together isometries. Variations within these families lead to "floppy modes" of deformation. Thin hyperbolic free sheets are thus easily deformed by weak stresses. The buckling pattern may be sensitive to the dynamics of the swelling process, experimental imperfections, or other external forces. A statistical description of the singularities and their interactions is therefore a natural approach to study this system.
References:
- Gemmer, J. A., & Venkataramani, S. C. (2011). Shape selection in non-Euclidean plates. Physica D: Nonlinear Phenomena, 240(19), 1536-1552.
- Gemmer, J. A., & Venkataramani, S. C. (2012). Defects and boundary layers in non-Euclidean plates. Nonlinearity, 25(12), 3553.
- Gemmer, J. A., & Venkataramani, S. C. (2013). Shape transitions in hyperbolic non-Euclidean plates. Soft Matter, 9(34), 8151-8161
- Gemmer, J., Sharon, E., Shearman, T., Venkataramani, S. C. (2016). Isometric immersions, energy minimization and self-similar buckling in non-Euclidean elastic sheets. EPL (Europhysics Letters), 114(2), 24003. Chicago
