| MWF 11-11:50 AM | OPL 107 | http://www.wfu.edu/~natalie/f05phy711/ |
| Instructor: Natalie Holzwarth | Phone:758-5510 | Office:300 OPL | e-mail:natalie@wfu.edu |
Read Chapter 1 in Fetter & Walecka and make note of useful appendices.
Continue reading Chapter 1 in Fetter & Walecka.
Finish reading Chapters 1 & 2 in Fetter & Walecka.
Continue reading Chapter 3 in Fetter & Walecka and also section 33 in Chapter 6.
Continue reading Chapter 3 in Fetter & Walecka.
Continue reading Chapter 3 in Fetter & Walecka.
Continue reading Chapter 3 in Fetter & Walecka.
Finish reading Chapter 3 in Fetter & Walecka.
Read Sections I-III of the paper by Hans C. Andersen on Molecular Dyanmics Simulations. Work through the equations to find the equations of motion 3.14, correcting any typos along the way.
Start reading Chapter 4 in Fetter & Walecka.
Work problem 4.2, parts a-c (d-e for extra credit) in Fetter & Walecka.
Finish reading Chapter 4 in Fetter & Walecka.
Work problem 4.9 OR problem 4.12 (extra credit for working both) in Fetter & Walecka.
Start reading Chapter 5 in Fetter & Walecka

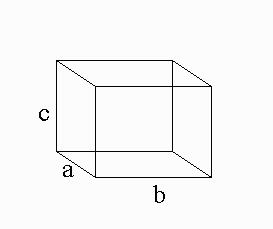
Consider the rectangular solid shown in the diagram. Assume that it has a uniform mass distribution and that the lengths a, b, c are not equal.
Continue reading Chapter 5 in Fetter & Walecka.
Continue reading Chapter 5 in Fetter & Walecka.
Start reading Chapter 6 in Fetter & Walecka.
Continue reading Chapter 7 in Fetter & Walecka.
Continue reading Chapter 8 in Fetter & Walecka.
Start reading Chapter 9 in Fetter & Walecka.
Continue reading Chapter 9 in Fetter & Walecka.

Continue reading Chapter 9 in Fetter & Walecka.
Continue reading Chapter 9 in Fetter & Walecka.
Continue reading Chapter 9 in Fetter & Walecka.
Consider the example shown in Fig. 51.1 which results in the power distribution given in Fig. 51.19. Estimate reasonable values for the parameters and plot the distribution as a function of angle. Find the angles of zero power.
Continue reading Chapter 9 in Fetter & Walecka.
Consider an ideal monoatomic ideal gas moving as a non-linear traveling wave as discussed in Section 52 of your text. For this value of γ and your choice of waveform, determine the time for the onset of "shock" formation.
Finish reading Chapter 9 in Fetter & Walecka.
Continue reading Chapter 10 in Fetter & Walecka.
Work problem 10.3 in Fetter & Walecka.
Finish reading Chapter 10 in Fetter & Walecka.
Using the Soliton lecturenotes, find one or two of the terms eliminated from the equation and estimate their magnitudes relative to the terms kept in Eq. (24), in terms of the soliton solution.
Start reading Chapter 11 in Fetter & Walecka.
Work problem 11.1 in Fetter & Walecka.
Continue reading Chapter 11 in Fetter & Walecka.
Use Laplace transforms to find the trajectory Y(t) given an initial position Y(0) and initial velocity V(0) and constant acceleration Ÿ(t)=-g.