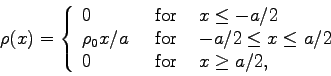
where
- Solve the Poisson equation for the electrostatic potential
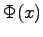 with the boundary conditions
with the boundary conditions
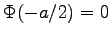 and
and
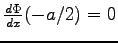 .
.
- Find the corresponding electrostatic field
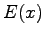 .
.
- Plot
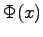 and
and 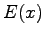 .
.
- Discuss your results in terms of elementary Gauss's Law arguments.
| MWF 10-10:50 PM | OPL 107 | http://www.wfu.edu/~natalie/s09phy712/ |
| Instructor: Natalie Holzwarth | Phone:758-5510 | Office:300 OPL | e-mail:natalie@wfu.edu |
Read Chapters I and 1 in Jackson. The following problem will be due Fri, Jan. 16, 2009.
Continue reading Chapters 1 in Jackson. Homework due Fri. Jan. 23, 2009.
Continue reading Chaper 1 & 2 in Jackson; homework is due Monday, Jan. 26, 2009.
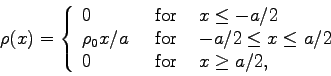
Continue reading Chaper 1 & 2 in Jackson; homework is due Wednesday, Jan. 28, 2009.
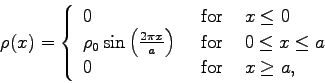
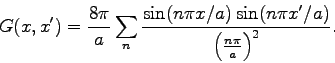
Continue reading Chaps. 1-3 in Jackson. The following problem will be due Fri, Jan. 30, 2009.
Continue reading Chaps. 2 in Jackson. The following problem will be due Mon, Feb. 2, 2009.
Review last section of Chap 1 in Jackson . This problem is due Feb. 4, 2009
Finish reading Chapters 1-2 in Jackson . This problem is due Feb. 6, 2009.
Start reading Chapter 3 in Jackson . This problem is due Feb. 9, 2009.
Finish reading reading Chapter 3 in Jackson . This problem is due Feb. 11, 2009.
Finish reading reading Chapter 4 in Jackson . This problem is due Feb. 20, 2009.
Start reading Chapter 5 of Jackson. This problem is due Monday Feb. 23, 2009.
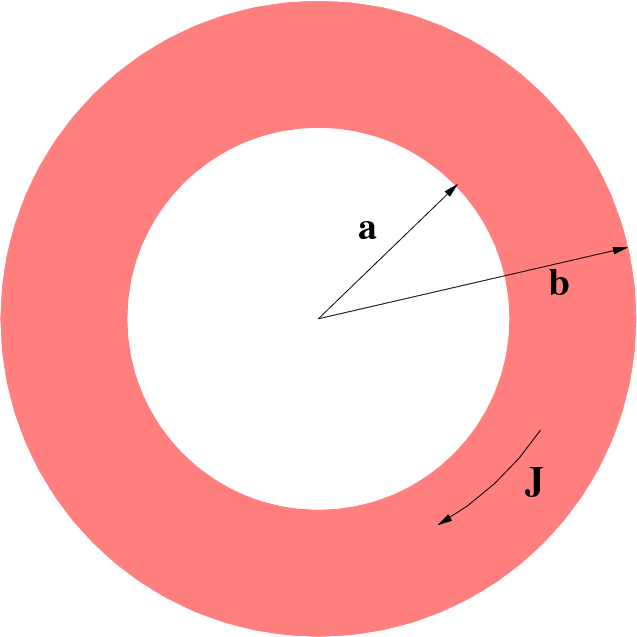
The figure above shows the cross section of a
magnetostatic solenoid which is uniform in the
![]() direction (perpendicular to the page). The current flows in the azimuthal
direction (perpendicular to the page). The current flows in the azimuthal
![]() direction; specifically the
current density is given in cylindrical coordinates by:
direction; specifically the
current density is given in cylindrical coordinates by:
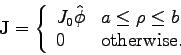 |
(1) |
| (2) |
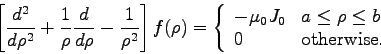 |
(3) |
Continue reading Chap. 5 in Jackson. The following problem will be due Wed. Feb. 25, 2009.
Finish reading Chap. 5 in Jackson. The following problem will be due Mon. Mar. 2, 2009.
Start reading Chapter 6 of Jackson. The problem will be due Wed. Mar. 4, 2009.
| (1) |
| (2) |
Assuming solutions of the form:
| (3) |
Continue reading Chapter 6 of Jackson. This problem will be due Wed. March 25, 2009.
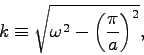
Start reading Chapter 7 in Jackson . This problem is due Friday, March 27, 2009.
Continue reading Chapter 7 in Jackson . This problem is due Monday, March 30, 2009.
Continue reading Chapter 7 in Jackson . This problem is due Wednesday, April 1, 2009.
Continue reading Chapter 7 in Jackson . This problem is due Friday, April 3, 2009.
Start reading Chapter 11 in Jackson . This problem is due Monday, April 6, 2009.
Continue reading Chapter 11 and start reading Chapter 14 in Jackson . This problem is due Monday, April 13, 2009.
Continue reading Chapter 14 in Jackson . This problem is due Wednesday, April 15, 2009.
Continue reading Chapter 14 in Jackson . This problem is due Friday, April 17, 2009.
Finish reading Chapter 14 and start Chapter 9 in Jackson
Continue reading Chapter 9 of Jackson. This homework is due Wed. Apr. 22, 2009.
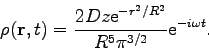
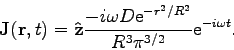
Finish reading Chapter 9 and start Chapter 10 in Jackson. This problem is due Friday, Apr. 24, 2009.