| MWF 11-11:50 AM | OPL 107 | http://www.wfu.edu/~natalie/f08phy711 |
| Instructor: Natalie Holzwarth | Phone:758-5510 | Office:300 OPL | e-mail:natalie@wfu.edu |

Continue reading Chapter 1 in Fetter & Walecka.
Continue reading Chapter 1 in Fetter & Walecka.
Skim Chap. 2 and start reading about the calculus of variation in Chap. 3 in Fetter & Walecka.
![\begin{displaymath}I = \int_0^1 \left[ \left( \frac{dy}{dx} \right)^2 + \frac{y}{a} \right], \end{displaymath}](./hw5/img2.png) |
(1) |
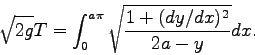 |
(1) |
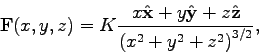
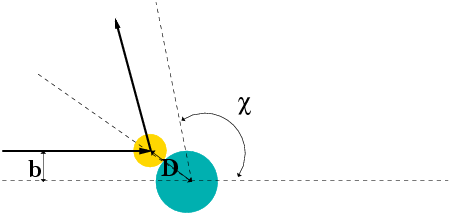
This exercise is designed to illustrate the differences between partial and total derivatives.
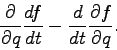
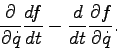
Continue reading Chapter 3 in Fetter and Walecka.
Consider the following Lagrangians. For each, determine the equations
and constants of
motion.
Assume that ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are constant parameters.
are constant parameters.
Start reading Chapter 6 in Fetter & Walecka.
Continue reading Chapters 6 in Fetter & Walecka.
Finish reading Chapter 6 in Fetter & Walecka.
Read parts of the paper by Hans C. Andersen "Molecular dynamics simulations at constant pressure and/or temperature" in which he constructs a Lagrangian function to represent a system of particles held at constant pressure α.
Finish reading Chapter 5 in Fetter and Walecka.
In most Classsical Mechanics texts (besides Fetter and Walecka), the Euler angles are defined with a different convention as shown below. (This figure was slightly modified from one available on the website http://en.wikipedia.org/wiki/Euler_angles.)
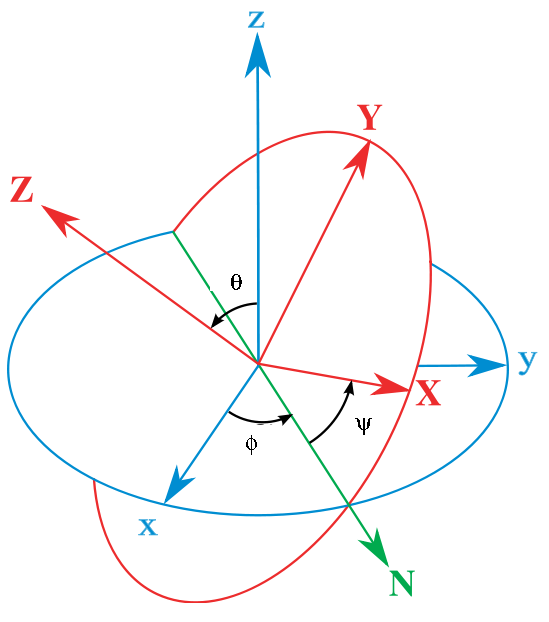
In this case, the first rotation is about the original ![]() axis by
axis by ![]() corresponding to the rotation matrix
corresponding to the rotation matrix
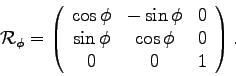 |
(1) |
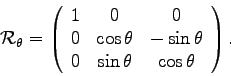 |
(2) |
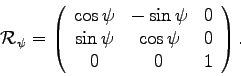 |
(3) |
Start reading Chapter 7 in Fetter and Walecka.
Suppose that an infinite continuous string satisfies the wave equation:
| (1) |
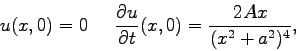 |
(2) |
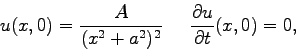 |
(3) |
You can visualize your results using the animate feature of Maple. For example, to animate the result we obtained in class today, you can use the following syntax:
> with(plots); > animate(plot, [exp(-(x+t)^2)+exp(-(x-t)^2), x = -30 .. 30], t = 0 .. 20);
Continue reading Chapter 7 in Fetter & Walecka.
Continue reading Chapter 7 and also Appendix A in Fetter & Walecka.
Continue reading Chapter 7 in Fetter and Walecka.
Consider the differential equation
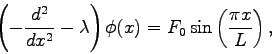 |
(1) |
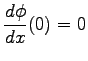 and where
and where 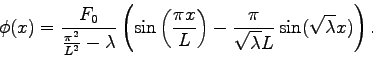 |
(2) |
Start reading Chapter 9 in Fetter & Walecka.
Continue reading Chapter 9 in Fetter & Walecka.
Continue reading Chapter 9 in Fetter & Walecka.
Continue reading Chapter 9 in Fetter & Walecka.
Finish reading Chapter 9 and start 10 in Fetter & Walecka.
Continue reading Chapter 10 in Fetter & Walecka.
Continue reading Chap. 10 in Fetter & Walecka. The following problem uses material from the end of Chap. 10 and the lecturenotes on solitary waves.
In class and in the lecture notes, we derived the soliton form of the surface displacement given by ζ(x,t)=η(x-ct) expressed in Eq. 25 of the notes. From this result find the following quantities to lowest order in &eta0/h, the ratio of the wave amplitude to the water depth.
Finish reading Chap. 12 in Fetter & Walecka.
Finish reading Chap. 11 in Fetter & Walecka.
Finish reading Chap. 13 in Fetter & Walecka.